This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Maryam Mirzakhani died July 14. She was a prominent mathematician and had rocketed into the spotlight in 2014 when she became the first woman and first Iranian to be awarded the prestigious Fields Medal. She was only 40. She was should have had years ahead of her. Her death is a huge loss to the mathematical community.
Obituaries of Mirzakhani, including the one I wrote, tend to mention her interest in both hyperbolic geometry and billiards. What’s less clear in those articles is how those two areas are linked. In short, we can link the two areas by unfolding a billiards table into a surface that can support hyperbolic geometry.
Hyperbolic geometry is the study of surfaces whose natural geometry is saddle-shaped everywhere. Locally, objects that are two-dimensional, like the surface of a beach ball or bagel, can have one of three different kinds of geometry: positive (curved like a sphere), negative (curved like a saddle or Pringles chip), or flat (like a piece of paper or tabletop). Furthermore, surfaces can be classified by what kind of geometry is “natural” for the entire object. A bagel that sits in our real three-dimensional world has some spots that are ball-like and some spots that are saddle-like, but as an abstract surface, its “natural” geometry is actually flat. One way to see that is that you can build a bagel-like shape, or torus, from a flat piece of paper by gluing the edges together. See this article about the torus for more information.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Objects with no holes, like a beach ball, are naturally positively curved (also known as spherical geometry), and objects with lots of holes, like pretzels, have natural negative curvature (also known as hyperbolic geometry). Mirzakhani studied surfaces with lots of holes.
Those surfaces often came from billiards tables. Although mathematicians care about billiards tables in many different shapes, we might as well start with the rectangular table and see how we can get from a flat rectangle with billiards balls bouncing around on it to a surface, in this case a torus. I wrote about that in an article about one of my favorite spaces, two tori glued along a slit, so this explanation is adapted from that article.
Mathematical billiards are idealized. No friction will slow them down. Instead of a ball with some large area, a single point travels in a straight line until it hits the side of the table, at which point it has a perfectly elastic collision with the side and continues along its way in another direction. (The angle of incidence is the angle reflection, so if it hits the side of the pool table head on, it will be reflected back in the same direction. If it hits at a 30° angle, it will bounce off at a 30° angle.)
All that bouncing around and changing directions make it complicated to keep track of the trajectory, so mathematicians employ a clever trick to make their questions easier: they unfold the table. When the ball hits the side, instead of the ball’s trajectory being reflected, we reflect the table, and the ball continues unhindered. That way the direction stays the same forever. To see how this works for a rectangle, we’ll follow a point around to see what happens.
First, we start out moving northeast in a rectangle. I marked the rectangle with a little L in the bottom left corner so we can keep track of the orientation of the table as we unfold it.
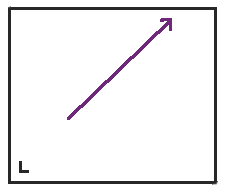
When we get to the top of the rectangle, instead of bouncing back, we reflect the table across the top, and the point continues on its way.
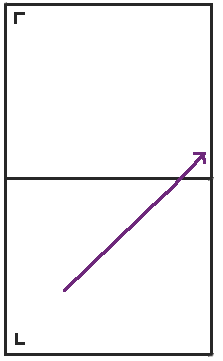
When we reach the right side of the table, we reflect the table across the right side and keep going.

When we get to the top of that table, we reflect again.
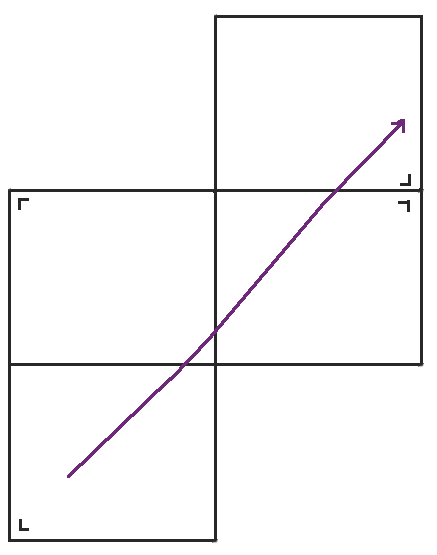
When we reach the right side, we could reflect the table again, but the bottom left table has the same orientation as the table we would get, so we might as well jump back down to the bottom left table again instead. When we rearrange the table a little bit, we get our familiar torus, a rectangle with the top glued to the bottom and the left side glued to the right side.

Here's the whole process as a gif.
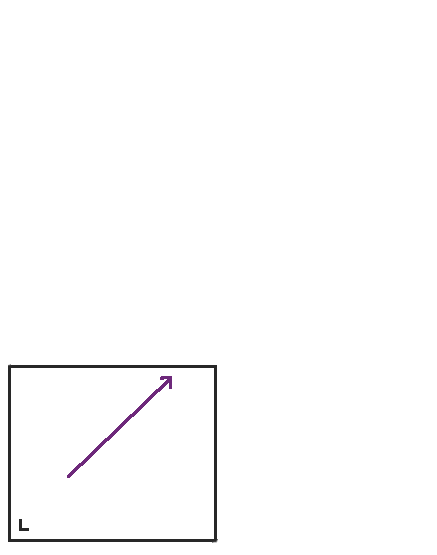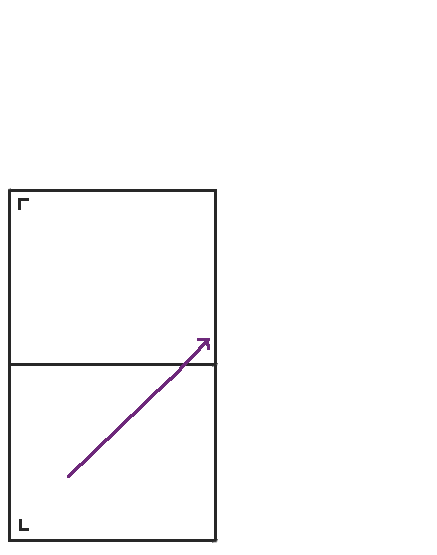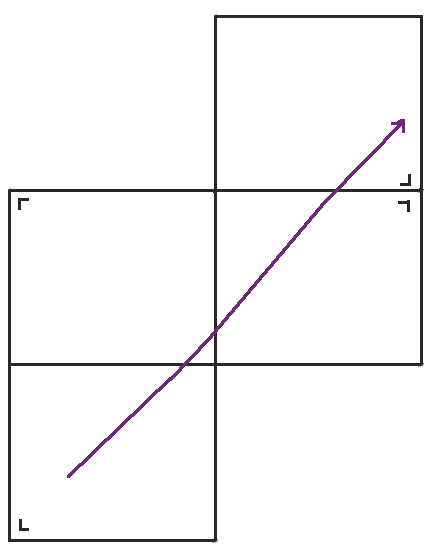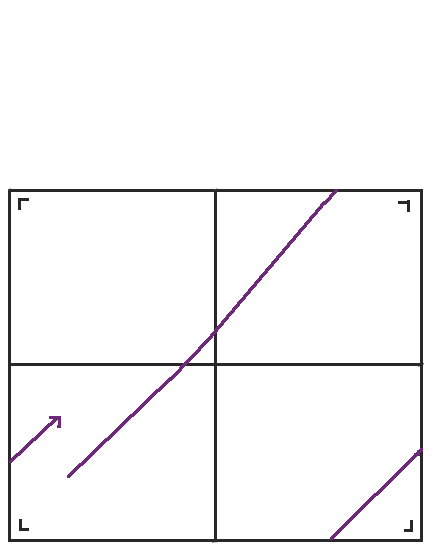
In this way, we get from billiards on a rectangle to straight-line flows on a torus. I saw this unfolding demonstration a few times in graduate school, and I felt pretty confident that I understood it. But the rectangle is a simple shape. And in the end, it unfolds into a surface that is naturally flat. Could I do this unfolding procedure and get a surface that is naturally hyperbolic? In the next post, I'll write about what happened when I tried to unfold a pentagonal pool table.