This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Annalisa Crannell goes to art museums with chopsticks. She is not unusually hungry or over-prepared; she uses them to figure out how to look at the art.
Crannell, a mathematician at Franklin and Marshal College in Lancaster, Pennsylvania, studies mathematical perspective and applies her work to the world of art. She writes not only about how artists use perspective but also about how viewers can use it to see art in different ways.
In a 2014 Math Horizons article (pdf, also available in The Best Writing on Mathematics 2015, edited by Mircea Pitici), she and coauthors Marc Frantz and Fumiko Futamura take on the case of the mysterious table in 15th- and 16th-century German artist Albrecht Dürer’s famous engraving St. Jerome in His Study.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

St. Jerome in His Study, by Albrecht Dürer. Public domain, via Wikimedia Commons.
This work is an early example of mathematical perspective in art, but some critics have maligned Dürer’s technique. William Mills Ivins Jr., a former curator at the Metropolitan Museum of Art in New York, described it as “the oddest trapezoidal shape” and claimed it wasn’t even level with the floor. Crannell and her coauthors say it’s a matter of perspective. They write, “Surprisingly, the answers to these questions depend not only on what Dürer did 500 years ago, but also on what Ivins did in 1938. And, as we will show, it depends on what you, the reader, do when you look at St. Jerome today.”
Crannell and her coauthors describe how to use straight lines in St. Jerome in His Study to determine exactly where the viewer should stand to see the painting from the perspective Dürer probably intended, and therefore to see the table as a square instead of a trapezoid. The proper viewing location for that particular engraving turns out to be closer to the picture and farther to the right than most people would naturally stand. They write, “The oddness that Ivins saw in the table wasn’t because Dürer was in the wrong, but because Ivins was in the wrong, literally: he was looking from the wrong place!”
In February, I had the pleasure of going to the Brigham Young University Museum of Art with Crannell, and she shared some of her secrets with me. (The BYU Museum of Art does not normally allow photography, so I thank them for graciously making an exception for us.)
In perspective art, lines in the painting that represent parallel lines in the real world—say, train tracks or the opposite sides of a table—intersect on the canvas at so-called vanishing points. These vanishing points are the key to determining the optimal location from which to view a painting.
The most obvious way to find the vanishing points of a painting and thus to determine the optimal viewing location is to place rulers directly on “parallel” lines in the drawing, but shockingly, most museums frown on that practice. That’s where the chopsticks come in.

Image: Evelyn Lamb.
Standing in front of a piece of art, Crannell closes one eye and holds the chopsticks in front of her so they line up with lines in the artwork that represent parallel lines in the real world. The place the chopsticks appear to intersect is in front of the vanishing point of those lines. For art that has one vanishing point, the viewer should stand directly in front of that point. The viewing distance can be determined by trial and error or by some sneaky geometry with squares.
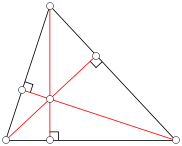
A diagram illustrating the orthocenter of a triangle. Each red line is one altitude of the triangle. Image: Public domain-self, via Wikimedia Commons.
For art with two vanishing points, the optimal viewing point is somewhere on the semicircle that connects the two vanishing points. For three vanishing points, determining the optimal vantage point is a bit more involved. It is at the intersection of three hemispheres, each one of which has two of the vanishing points as a diameter. Equivalently, it is somewhere in front of the orthocenter of the triangle whose vertices are the vanishing points. (The orthocenter of a triangle is the intersection point of the three altitidues of the triangle, as illustrated in the diagram on the right.) For a more complete description of how to find viewing points in art, check out Viewpoints: Mathematical Perspective and Fractal Geometry in Art by Crannell and Frantz.
In addition to giving me a way to look eccentric at the museum, Crannell’s technique helps me understand why some paintings seem to leap off the page, and some, even though they basically look realistic, don’t quite pop. In some pieces we looked at, lines that should have represented parallel lines in the real world didn't end up determining a consistent vanishing point. Looking at any one part of the painting, nothing was clearly wrong, but the overall effect was slightly imperfect. When artists do manage to deploy perfect perspective—and viewers manage to find the correct vantage point—the effect can be startlingly realistic.
As Crannell and her coauthors describe it,
we can see the effect that the master geometer Albrecht Dürer intended. If you view St. Jerome in His Study [from the mathematically determined vantage point], you’ll see that the engraving takes on an amazing realism and depth. The gourd in the picture seems to hover over your head; you feel you could stick your hand in the space under the table; the bench off to the left invites you to come sit down and fluff up the pillows.
If you would like to know how to find those fluffy pillows for yourself, Crannell has information about projective geometry and perspective art on her website.
