This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
The digits of pi reciting contest is an all-too-common Pi Day event. And as this year is a once-in-a-century confluence of month/day/year with the first few decimal digits of pi, we might be in for more of those than usual. Our 10 fingers make decimal digits a natural choice, but if we were capybaras or the Simpsons, we might use base 8. If we were ancient Mesopotamians, we would use base 60. Memorizing the digits in any of these bases is a bit arbitrary. The decimal, octal, and sexagesimal digits of pi don't capture the true essence of pi-ish-ness. Why not have a contest that has all of the rote memorization fun of decimal digit recitation with none of the arbitrary base dependence? That's right, this year you need to have a continued fraction reciting contest!
"Sounds great," I can hear you saying, "but what does that mean?" I'm glad you asked! A couple years ago, I blogged about continued fractions, the most romantic way to represent numbers. As I wrote then, a continued fraction is like a fraction but more so. Instead of stopping with one number in the numerator and one in the denominator, the denominator has a fraction in it too. And the denominator of that fraction has a fraction in it, and so on.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
To standardize continued fractions, we require every numerator to be 1 and every denominator to be positive. (We'll also allow ourselves to add an arbitrary positive or negative integer to the front of the continued fraction, so we can represent numbers that are not between 0 and 1.)
With these restrictions, every number has a (basically) unique continued fraction representation. If the number is rational, the continued fraction eventually terminates. If it's irrational, the continued fraction continues forever.
Although we write the denominators of continued fractions using decimal notation, continued fractions are not base dependent. 12 is the same number whether we write it as 12 base 10 (decimal), 1100 base 2 (binary), or C base 16 (hexadecimal). So if twelve is in the denominator of a continued fraction, it doesn't matter what base we write it in. The continued fraction representation of a number has the same numbers in it, perhaps written a different way, no matter what base we use.
The continued fraction expansion of a number x tells us which rational numbers, or fractions, are the best approximations of x. When we truncate the continued fraction after a certain number of terms, we get what is called a convergent to x. If the convergent has the denominator n, that means no number with a smaller denominator than n is closer to x. Convergents are best approximations in an even stronger sense, but that's a topic for another time. Suffice it to say that convergents are the best of the best approximations, the cream of the approximation crop.
For a concrete example, let's look at the number pi. The continued fraction for pi is:
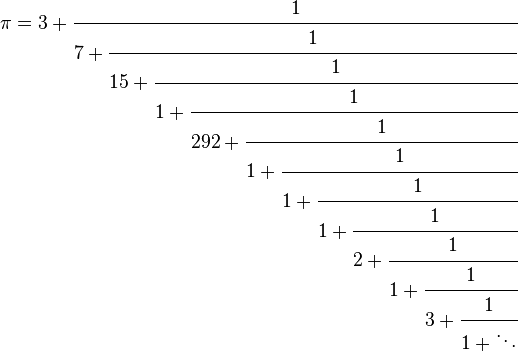
The continued fraction expansion for pi.
And the first few convergents are: 3 (duh), 22/7 (Pi Approximation Day), 333/106, 355/113, and 103,993/33,102. After 22/7, all of the convergents are better approximations of pi than 3.1415, which corresponds to the date of Pi Day this year. In fact, 355/113 is accurate to two more decimal places than 3.1415, with only three digits in the denominator instead of five (if you think of 3.1415 as 31,415/10,000). With efficiency like that, why bother with decimal digits at all? While everyone else is celebrating "the only Pi Day of our lives," you should make sure to tell them that 3.1415 is not a very good approximation of pi. Just try to avoid saying it at 9:26.

Zoidberg agrees: 3.1415 is a suboptimal approximation of pi. Image made by me at memegenerator.net.
A continued fraction reciting contest is a much better way of celebrating pi than reciting its decimal digits. Instead of wasting your time with numbers that correspond to mediocre approximations of pi, you'll only be mentioning numbers that correspond to really good approximations of pi. The big dilemma is whether you should recite the list of denominators in the continued fraction (sequence A001203 at the Online Encyclopedia of Integer Sequences) or its convergents, the fractions themselves that best approximate pi. Convergents are a little trickier: the numerators are in integer sequence A002485 and the denominators are in sequence A002486. Reciting the denominators of the continued fraction is a more analogous activity to a digit reciting contest, but the convergents offer more of a challenge!
I do feel compelled to point out that besides base 10 being an arbitrary way of representing pi, one of the reasons I'm not fond of digit reciting contests is that, to steal an analogy I read somewhere, memorizing digits of pi is to math as memorizing the order of letters in Robert Frost's poems is to literature. It's not an intellectually meaningful activity. A continued fraction reciting contest isn't any better than the digit reciting contest in that regard. If you'd like to celebrate Pi Day with an activity that is more inherently mathematical, check out last Pi Day's post on Math Munch, which includes instructions for estimating pi using Buffon's needle or watch this fun video by the good folks at the Aperiodical in which several mathematicians employ various pi approximating strategies to mixed success. Or read my post from last year about π(x), the prime counting function, a different mathematical use of the symbol π. Whatever you do, have a good Pi Day!

