This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
I have an article in Slate today about Andrew Hacker’s bookThe Math Myth: And Other STEM Delusions. I’ve written before about Hacker’s thesis that there should be less math in the high school curriculum, but now that he has a book, there’s even more to argue with. The book is littered with examples that could have come from a book on mathematical illiteracy. As I wrote at Slate, “I almost hope they’re Easter eggs for numerate people and that Hacker has a secret agenda of improving math education to the point that everyone can recognize that his arguments are full of crap.”
There was a lot I didn’t get to in the Slate piece. For example, I left the book-throwingest line out. In a chapter about the gender gap, Hacker notes that some people think women aren't as good at math as men and then writes, “As it happens, debates about gender-based capacities don’t arise in other intellectual areas.” I just can't deal with that one, so I’ll let Amy Poehler handle it for me.

Really? Image: The Frisky
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
One of the other examples he gets wrong is pretty interesting, and once you get past the way Hacker distorts the story, it's fun to think about. Here Hacker writes about an exchange Jeb Bush had with some students.
When, as governor of Florida, he visited an Orlando high school, a student had a question for him: “What,” Luana Marques asked, “are the angles on a three-four-five triangle?” She wondered if he knew, since problems like this were on a statewide test, which she and some 140,000 high school seniors had just had to take. “I don’t know,” her governor confessed, “one hundred twenty-five, ninety and whatever remains on one hundred eighty?
Had a teenaged Jeb Bush muffed questions like that, he would have been denied a high school diploma under a statute he supported and signed. In fact, not three in a hundred adults could answer Ms. Marques’s question. (It’s not as easy as it might seem.)
Hacker isn’t telling us something here. The exchange did happen, but Marques wasn’t correct that the Florida Comprehensive Assessment Test (FCAT) she was referring to asked about the angles in a 3-4-5 triangle. I bet a lot of other math teachers immediately saw that error as well.
To be clear, it’s OK that a student misremembered something from a test and asked Bush about it. I have nothing against Marques here. But Hacker should know better. If he knows enough to tell us the answer isn’t as easy as it might seem, he should know enough to find out whether the question was on the test. (The fact that it wasn’t is documented.) Yet he conveniently leaves that part out. If he had included it, his story wouldn’t have supported the point he wanted it to. He simply wants people who haven’t seen trigonometry in a while to throw up their hands at a question they don’t know the answer to.
How did I know the question wasn’t on the test? The question isn’t difficult—the triangle is a right triangle, and some basic trigonometry gets you the angles—but teachers wouldn’t ask a student to answer this particular question about that particular triangle. There are a few exalted triangles that have easy-to-calculate side lengths and angles: equilateral triangles, isosceles right triangles, and 30-60-90 right triangles. In my experience, those are basically the only triangles you’re supposed to know both the angle measures and side lengths of.
The angles of the 3-4-5 right triangles are arcsin(4/5), arcsin(3/5), and 90 degrees. If it's been a little while since SOH CAH TOA, it's OK. The sine, cosine, and tangent of an angle represent relationships between the sides of a right triangle with that angle. A picture's worth a thousand words. The sine of the marked angle, α, is the ratio of the opposite side to the hypotenuse. If this is a 3-4-5 right triangle, the opposite side has length 4 and the hypotenuse has length 5.
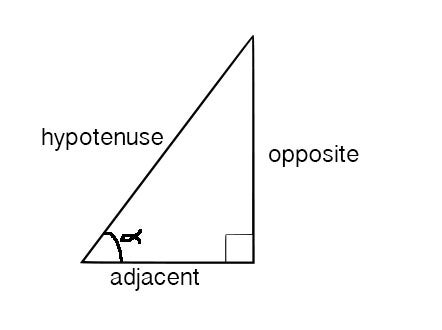
The problem is that we don’t think of something like arcsin(4/5) as a number. But arcsin(4/5) is a perfectly good number: it’s the angle whose sine is 4/5. (I can hear the pedants—I can say that because I am one myself—screaming that there are multiple angles with a sine of 4/5. We’re in the market for an angle between 0 and 90 degrees whose sine is 4/5, so let’s just find the one in that range and call it a day.) I think the fact that we have trouble thinking that way says something interesting about our psychological relationship to numbers. By the way, if you're getting nervous to see arcsin all over the place, the angle is about 53 degrees.
Nineteenth-century German mathematician Leopold Kronecker is quoted as saying, “God made the integers, all else is the work of man.” I think this is a good summary of how many people see numbers. Despite the fact that you can’t really touch any number, the whole numbers somehow feel more real to us than other numbers. We teach math in an integer-centric way, and when integers fail, we think of numbers as being more real when they're decimals and fractions rather than written in other ways. How many people know π is a number but feel more comfortable when they see it written as 3.14159...?
I know I've gone on a pretty long tangent about a question that didn't appear on the FCAT, but it's fun to think about how we think about numbers. Perhaps all (real) numbers are real, but some numbers are realer than others.