This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
How can you tell what your planet looks like? One way is to develop a space program, send vessels up, and take pictures of it from far away. Several cameras and a very small percentage of humans have left the planet to look at it from space, and they say it looks like a sphere. But what if they’re lying? While a recent paper suggests it would be difficult to sustain a global conspiracy of all space agencies, astronauts, and planetary scientists, we don’t have to take their word for it.
Instead of developing a space program, there’s a mathematically clever, practically impossible way to figure out what kind of surface we live on: the Euler characteristic. (This is one of many entries on the list of things named after Leonhard Euler.) Humans knew the earth was a sphere long before space programs, or even Columbus, existed. This is not how they figured it out.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
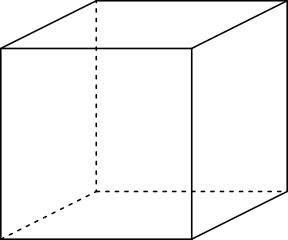
Like age, the Euler characteristic is just a number. For a two-dimensional surface like a box, beach ball, or planet, it is the number of vertices of an object minus the number of edges plus the number of faces, or V-E+F. We’ll start with a simple example, a cube. A cube has 8 vertices, 12 edges, and 6 faces, so the grand total is 8-12+6=2.
What about a sphere? Here, the vertices and edges don’t come for free. We have to draw them in. One way to do that is to draw an equator and some meridians on a globe. Or, if you don’t have a globe, put rubber bands around a grapefruit.

I don’t have a spherical camera, so if you don’t have your own grapefruit, you’ll have to take my word for it that there are 6 vertices where the rubber bands meet,12 line segments, and 8 triangles, for an Euler characteristic of 6-12+8=2. (The numbers happen to be similar to the numbers for the cube. Can you figure out why?)
It’s always dicey to make choices while you’re carrying out a computation. We made choices about how to put rubber bands on the grapefruit. What if we had done it differently? This time I put four rubber bands on it.

Now it has 10 vertices, 21 edges, and 13 faces, for, once again, 10-21+13=2.
In fact, no matter how we break the sphere up by drawing lines or putting rubber bands on it, we will end up with 2 for the Euler characteristic.* You don’t have to take my word for it. An airtight proof is a little involved, but you can easily convince yourself by doodling. Draw a shape and some vertices and edges inside it. Add a vertex and some edges. What happens to the Euler characteristic? Erase an edge. Now what happens?
The Euler characteristic is a topological invariant, meaning stretching or squishing the object won’t change it, only tearing or gluing will. The Euler characteristic, then, can be used to determine the topology of a surface but not its finer features. For example, the cube, sphere, tetrahedron, and other closed shapes like them all have the same Euler characteristic because they’re all topologically equivalent.
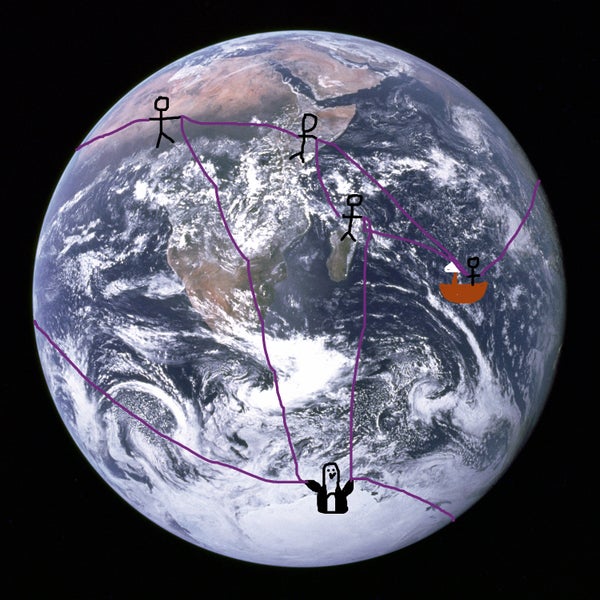
If you are a scientifically curious person who has not had the opportunity to go into space to see the earth for yourself and you don’t want to take ancient scientists’ or NASA’s word for it, you can use the Euler characteristic to determine the topology of the planet. All you need is several friends and a lot of rope.
Everyone stands at a point on the earth, and each person holds the ends of a few ropes. Now you count how many people there are, how many segments of rope there are, and how many regions are closed in those segments of rope. Then find the Euler characteristic, V-E+F.
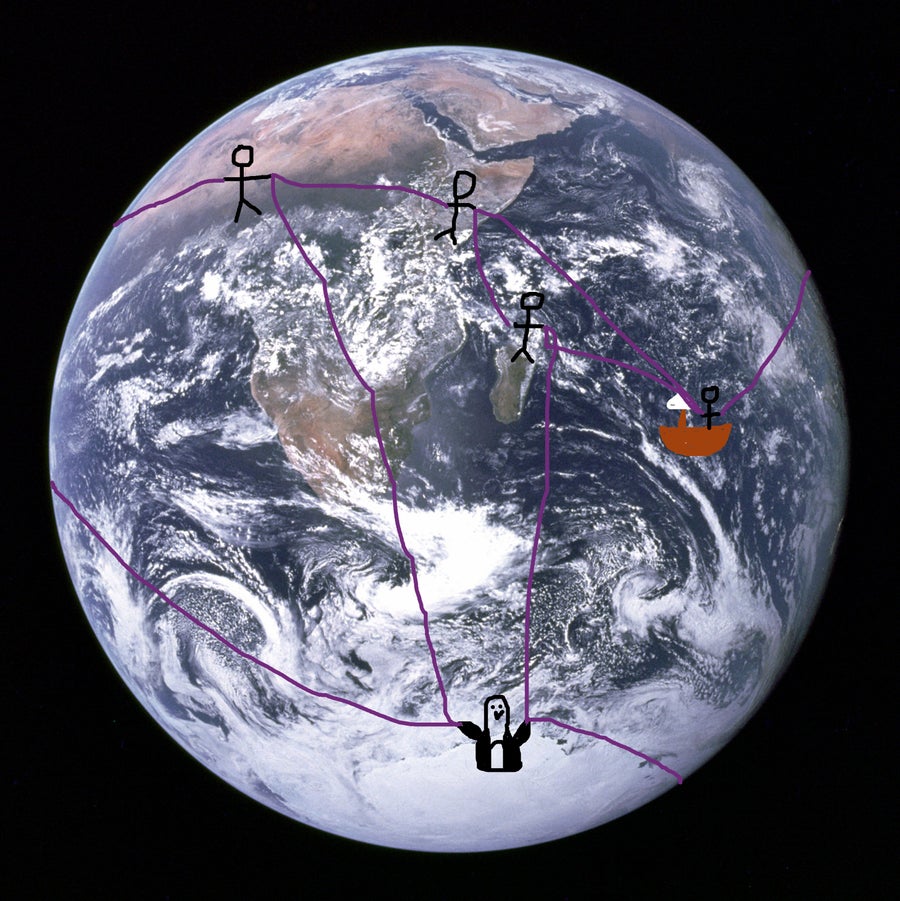
Not to scale.
If you got a 2, you’re done. Topologically, the only surface with Euler characteristic 2 is a sphere.
If you didn’t get 2, you probably miscounted. But let’s say you’re on an alien planet whose topology has not been determined. A few other aspects of the planet will help you determine exactly what surface it is.
First, is the world finite, or does it go off forever into the abyss? If the world is infinite, you can’t divide it up into sections and find an Euler characteristic, so you’re out of luck. We'll assume all worlds are finite.

A Möbius band. Image: David Benbennick, via Wikimedia Commons.
Next, we want to deal with orientability. The Möbius band is the most famous non-orientable surface: if you keep walking around it, you’ll eventually end up where you started but on the other side of the paper. With orientable surfaces, you know there’s an inside and an outside; you’ll never wander back to your starting place upside down. Whether or not your planet is orientable, you can use the Euler characteristic to figure out its topology.
Finally, boundaries. Do you think it’s possible to walk off the edge of the world? If so, how many separate edges are there? There could just be one going around the outside or there could be more. Perhaps you have reason to believe the earth is shaped like a washer or a fattened up figure 8.
The Euler characteristic, orientability, and number of boundary pieces uniquely determine what surface your planet is. If you get 2, you’re definitely on a sphere. Adding one boundary piece decreases the Euler characteristic by 1, so if you get a 1, you are on a sphere that got punctured, which is topologically equivalent to a polygon in the plane. If you get a 0, you could be living on a torus, or you could be living on a washer. The list goes on.
Once you know what your planet looks like topologically, you can start figuring out its geometry. If you got a 2, you can try to find out whether you live on a sphere, a cube, a football, or some other exotic surface. The Euler characteristic won’t help you there. I’d suggest you take a page from Eratosthenes and other ancient astronomers and start using shadows to determine how curved the earth is at any particular point. Ethan Siegel can tell you all about that.
Acknowledgements: I first encountered the idea of determining your planet’s topology using the Euler characteristic in a talk by my pal University of Utah mathematician Kevin Wortman. B.o.B. and Neil deGrasse Tyson inspired me to finish writing the post.
*In response to a comment, I will add the caveat that the regions you enclose can't have holes in them. That is, they should be like disks, not washers. The technical term is "simply connected." One way to ensure all the regions are simply connected is to triangulate your surface.