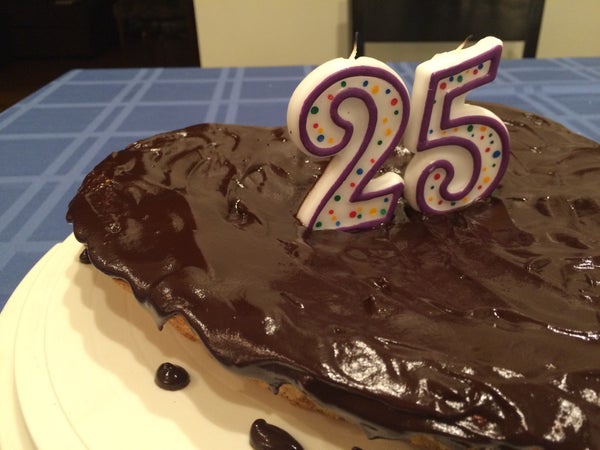This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
It was my birthday recently, so I started thinking about birthday candles. Once you’re past a certain age, individual birthday candles become a nuisance, not to mention a fire hazard, so those big number candles are a safer choice. But it’s such a hassle to buy new candles for every different age you or your friends turn. Today I’m going to tell you how you can save money and impress/confuse your friends by exploiting a little-known birthday candle loophole: they don’t specify the numerical base you have to use.
Mathematically, the base is kind of like the language you choose to write your numbers in. You can choose base 10, or decimal, and be just like the other
sheeplehumans who inhabit your society, or you can branch out. Binary (base 2) and hexadecimal (base 16) are popular options due to their utility in computing, but you can pick any number you want. (In fact, you don't even have to choose a whole number, but we'll just think about whole numbers today.) No matter what number you pick as a base, you can write numbers using the same basic idea: place value. The furthest right place represents ones, the next place to the left represents the base, the next place is the base squared, and so on.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
An example is worth a thousand explanations. In base 10, the number 513 means 3 ones, 1 ten, and 5 one-hundreds (102s). If we interpret the number in base 16 instead, 513 means 3 ones, 1 sixteen, and 5 two hundred fifty-sixes (162s), so it’s much larger. (In base 10, we’d describe that number as 1299.) The number 513 does not appear in binary because binary only uses the digits 0 and 1.
It’s just a custom that we mean the number ten when we write 10, or twenty-seven when we write 27. Without any indication to the contrary, we always assume numbers are written in base 10, but why should a birthday cake have to conform to this rigid custom anyway?
If you’ve decided to eschew base 10 for your birthday candles, you’ve got a decision in front of you: what number should you use on your birthday cake to represent your age? There’s a case to be made for putting a "10" on your cake. It’s simple to figure out what base you're using in that case. You’re turning 28? That’s 10 in base 28. You’re turning 87? That’s 10 in base 87. No muss, no fuss. But—and perhaps this is my decimal bias showing—10 looks so juvenile. You could pick a larger number that starts with a 1. 18 or 19 would look more grown-up. If you’re turning 28, you could put "18" on your cake and interpret it in base 20. If you’re turning 87, that’s 18 in base 79. But 18 and 19 still feel a bit young. To be honest, I thought and did a lot of silly and embarrassing things as a teenager, and I don’t really need to be reminded of them on my birthday.
Instead, I decided to go with 25 for my birthday candles this year. Using a 2 instead of a 1 as the first digit complicates things a bit, but 25 looks good to me. I was pretty happy at age 25 (base 10), and it saves me from the embarrassment of remembering myself as a teenager. The complication is that I won’t be able to reuse the candles next year. My age is an odd number this year, which means I can write it as 25 in some base. (No matter what base you use, “25” will always represent an odd number because it is 5 more than twice a whole number.) Next year, I’ll have to get an even number for the second digit, but at least I can reuse the 2. Besides, it would be monotonous to use the exact same number every year. Alternating between two numbers will be much less boring.
Why bother applying mathematics to birthday candles? To be honest, the vast* financial savings are probably not worth it. But it will also help endear you to the rest of the party guests. There’s nothing** fellow birthday party guests will appreciate more than the chance to learn a little bit about different numerical bases before singing “Happy Birthday.” Sarcasm aside, I've just always enjoyed writing numbers using alternative bases, and why should my birthday be any different?
*On the order of $0.99 per year.
**Except for eating the cake.