A Few of My Favorite Spaces: The Bicylinder

This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American

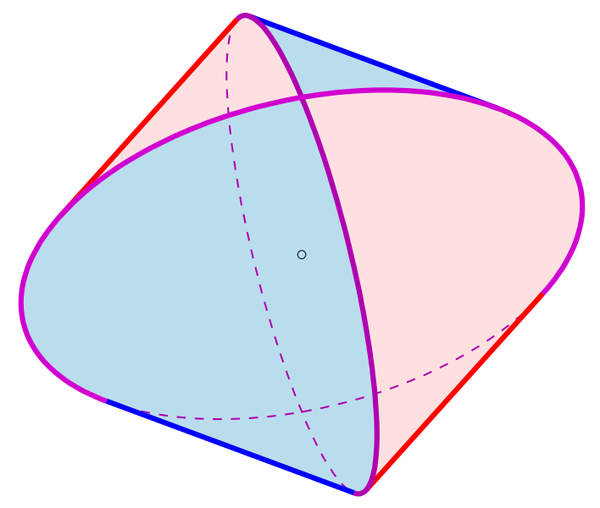
The bicylinder is a lovely little shape. It has square cross-sections, but it’s still pleasingly curved. It’s the shape you get if you look at the intersection of two identical solid cylinders that meet at right angles. Early Chinese mathematicians called the shape mouhefanggai, sometimes translated as “two square umbrellas,” and it is also known as the Steinmetz solid. (People also use the term Steinmetz solid to refer to a similar figure made from three or more, rather than two, intersecting cylinders.)

This object comes up in one of my favorite examples for Cavalieri’s principle. Cavalieri’s principle is the idea that if two objects have the same cross-sectional areas at every height, the two objects have the same volume. (Of course, there are some technicalities to keep straight to make sure we’re measuring the cross sections appropriately.) The idea seems obvious when you say it but can be counterintuitive when you see it in the wild. Calculus teachers love to use a stack of coins as an example. You can either arrange them neatly in a perfect cylinder or build a squiggly, wobbly tower from them. Either way, it’s the same stack of coins, so the two towers have the same volume. 

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

It’s not every day that you get to use Cavalieri’s principle in a computation, so it always feels a little bit special. Vsauce has a fun video about the napkin ring problem, a surprising application of the technique.

My favorite story about the bicylinder starts with Liu Hui, a Chinese mathematician who lived in the third century CE. He is most famous today for his extensive commentary on The Nine Chapters on the Mathematical Art, an important early Chinese mathematics text, and his algorithm for computing π using inscribed polygons. Liu used the bicylinder, or when he was investigating the area of a sphere.

One way to think about a sphere is as a stack of infinitesimally thin circles sitting on top of each other. The biggest circle is right in the middle, and they get smaller and smaller towards the poles.

To get a bicylinder, just replace each thin circle with a circumscribing square. To the best of my understanding, Liu came up with the bicylinder that way, looking for a shape that contained the sphere, rather than by looking at the intersection of two cylinders. But it’s not too hard to convince yourself that this stack of squares is the same as the intersection of two cylinders. To start, imagine putting a sphere in the middle of the bicylinder. Now imagine taking a cross-section of the bicylinder in the direction that cuts both cylinders in rectangles. Each cross-section will have a square of the bicylinder circumscribing a circle from the sphere. (If you’re having trouble visualizing it, you can always grab a couple of toilet paper tubes and make your own bicylinder.)

Like Liu, we can now notice that the cross-section of the mouhefanggai is always a square that circumscribes a circle. If we call the radius of the circle r, we can conclude that the ratio of areas of each cross-section of the bicylinder to the sphere is 4r²:πr², or 4:π. Now Cavalieri’s principle implies that the ratio of the volumes of the two objects is also 4:π.

Today, that feels sufficient. The volume formula for a sphere is familiar, so we can take it from there. If a sphere has volume 4/3πr³, we can conclude that the bicylinder has the volume 16/3r³.* But this isn’t where Liu started. He was actually trying to use the bicylinder to get a formula for the area of the sphere. Unfortunately, he got stuck there. But it was no small progress. As Lam Lay-Yong and Shen Kangsheng write in an article about Chinese use of Cavalieri’s principle, “Although Liu admitted that he could not proceed further with the proof of finding the volume of a sphere, he had analyzed the problem with mathematical rigor and had determined the areas of difficulty.” About 200 years after Liu's death, Zu Chongzhi and his son Zu Geng were able to pick up where he left off and finish computing the volume of the sphere using the bicylinder. Their approach involves clever decompositions of the cube circumscribing the bicylinder. 

For more information about the work of Liu Hui, Zu Chongzhi, and Zu Geng on determining the volume of the sphere, check out “The Chinese concept of Cavalieri’s principle and its applications” by Lam Lay-Yong and Shen Kangsheng or “An Old Chinese way of finding the volume of a sphere” by T. Kiang. (The former seems to be freely accessible; the latter may be behind a paywall.) You can also explore the bicylinder in some Geogebra worksheets by Anthony Or, one of which shows a little bit of the cube decomposition.

*This sentence was edited to correct an error in the volume of the bicylinder.

Read about more of my favorite spaces: The Cantor Set Fat Cantor Sets The Topologist’s Sine Curve Cantor's Leaky Tent The Infinite Earring The Line with Two Origins The House with Two Rooms The Fano Plane The Torus The Three-Torus The Möbius Strip The Long Line Space-Filling Curves The Wallis Sieve Two Tori Glued along a Slit The Empty Set The Menger Sponge The Connected Sum of Four Hopf Links Borromean Rings The Sierpinski Triangle Lexicographic Ordering on the Unit Square The SNCF Metric The Mandelbrot Set Fatou's Pancake The Pseudosphere The Douady Rabbit The Poincaré Homology Sphere The Kovalevskaya Top A 6-Holed Torus The Real Projective Plane The 1-Dimensional Sphere The Loch Ness Monster The Koch Snowflake