This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Is there a global theory for the shapes of fishes? It's the kind of thing I might feel encouraged to ask by my explorations of simple programs and the forms they produce. But for most of the history of biology, it's not the kind of thing anyone would ever have asked. With one notable exception: D'Arcy Wentworth Thompson.
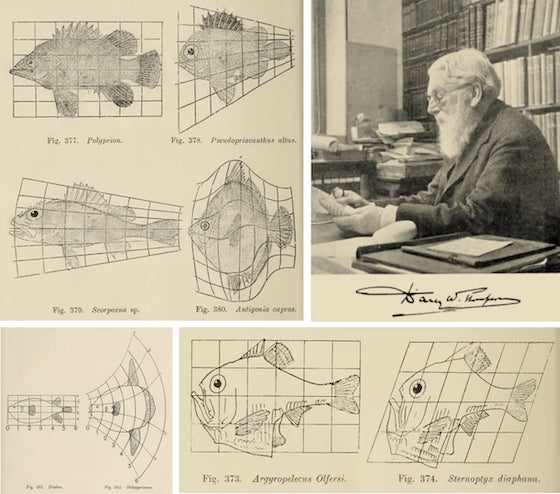
And it's now 100 years since D'Arcy Thompson published the first edition of his magnum opus On Growth and Form—and tried to use ideas from mathematics and physics to discuss global questions of biological growth and form. Probably the most famous pages of his book are the ones about fish shapes:
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Stretch one kind of fish, and it looks like another. Yes, without constraints on how you stretch, it's not quite clear what this is telling one, and I don't think it's much. But just to ask the question is interesting, and On Growth and Form is full of interesting questions—together with all manner of curious and interesting answers.
D'Arcy Thompson was in many ways a quintessential British Victorian academic, steeped in the classics, and writing books with titles like A Glossary of Greek Fishes (i.e. how were fish described in classical Greek texts). But he was also a diligent natural scientist, and he became a serious enthusiast of mathematics and physics. And where Aristotle (whom D'Arcy Thompson had translated) used plain language, with perhaps a dash of logic, to try to describe the natural world, D'Arcy Thompson tried to use the language of mathematics and physics.
At Christmas time, according to his daughter, he used to entertain children by drawing pictures of dogs on rubber sheets and stretching them from poodles to dachshunds. But it was not until the age of 57 that he turned such pursuits into the piece of scholarship that is On Growth and Form.
The first edition of the book was published in 1917. In many ways, it's like a catalog of biological forms—a kind of geometrical analog of Aristotle's books on natural history. It's particularly big on aquatic life—from plankton to fish. Land animals do make a showing, though mostly as skeletons. And ordinary plants make only specific appearances. But throughout the book the emphasis is on "why does such-and-such a thing have the form or shape it does?" And over and over again the answer that's given is: "because it's following such-and-such a physical phenomenon, or mathematical structure."
Much of the story of the book is told in its pictures. There are growth curves—of haddock, trees, regenerated tadpole tails, etc. There's a long discussion of the shapes of cells—and especially their connection with phenomena (like splashes, bubbles and foams) where surface tension is important. There are spirals—described mathematically, and appearing in shells and horns and leaf arrangements. And finally there's a long discussion of the "theory of transformations"—about how different forms (like the shapes of fishes or primate skulls) might be related by various (mathematically rather undefined) "transformations."

In D'Arcy Thompson's time—as still to a large extent today—the dominant form of explanation in biology is Darwinism: essentially the idea that things are the way they are because they've somehow evolved to be that way, in order to maximize some kind of fitness. D'Arcy Thompson didn't think that was the whole story, or even necessarily the most important part of the story. He thought instead that many natural forms are the way they are because it's an inevitable feature of the physics of biological tissue, or the mathematics of geometrical forms.
Sometimes his explanations fall a little flat. Leaves aren't really shaped much like polar plots of trigonometric functions. Jellyfish aren't convincingly shaped like drops of ink in water. But what he says often rings true. Hexagonal arrangements of cells are like closest geometrical packings of disks. Sheep horns and nautilus shells form logarithmic (equiangular) spirals.
He uses basic geometry and algebra quite a bit—and even sometimes a little combinatorics or topology. But he never goes as far as calculus (and, as it happens, he never learned it), and he never considers ideas like recursive rules or nested structures. But for me—as for quite a few others over the years—D'Arcy Thompson's book is an important inspiration for the concept that even though biological forms may at first look complicated, there can still be theories and explanations for them.
In modern times, though, there's a crucial new idea, that D'Arcy Thompson did not have: the idea of using not traditional mathematics and physics, but instead computation and simple programs as a way to describe the rules by which things grow. And—as I discovered in writing my book ANew Kind of Science—it's remarkable to what extent that idea lets us understand the mechanisms by which complex biological forms are produced, and lets us finish the bold initiative that D'Arcy Thompson began a century ago in On Growth and Form.
Who Was D'Arcy Thompson?
D'Arcy Wentworth Thompson was born in Edinburgh on May 5, 1860. His father, who was also named D'Arcy Wentworth Thompson, had been born in 1829, aboard a ship captained by his father, that was transporting convicts to Tasmania. D'Arcy Senior was soon sent to boarding school in England, and eventually studied classics at Cambridge. Though academically distinguished, he was apparently passed over for a fellowship because of perceived eccentricity—and wound up as a (modernizing, if opinionated) schoolteacher in Edinburgh. Once there, he soon met the lively young Fanny Gamgee, daughter of Joseph Gamgee, an early and distinguished veterinary surgeon—and in 1859 they were married.
D'Arcy (junior) was born the next year—but unfortunately his mother contracted an infection during childbirth, and died within the week. The result was that D'Arcy (junior) ended up living with his mother's parents, taken care of by one of his mother's sisters. When D'Arcy (junior) was three years old, his father then got a university professorship (of ancient Greek) in Ireland, and moved there. Still, D'Arcy (junior) stayed in close touch with his father through letters, and, later, visits. And indeed his father seems to have doted on him, for example publishing two children's books dedicated to him:

In a foreshadowing of his later interests, D'Arcy (junior) learned Latin from his father almost as soon as he was able to speak, and was continually exposed to animals of all sorts in the Gamgee household. There was also a certain math/physics theme. D'Arcy Thompson (senior)'s best friend in Edinburgh was Peter Guthrie Tait—a distinguished mathematical physicist (mechanics, thermodynamics, knot theory, ...) and friend of Maxwell, Hamilton and Kelvin—and D'Arcy (junior) often hung out at his house. Joseph Gamgee was also engaged in various scientific pursuits, for example publishing the book On Horseshoeing and Lameness based in part on a statistical study he'd done with the then 10-year-old D'Arcy (junior). Meanwhile, D'Arcy Thompson (senior) began to travel, as D'Arcy (junior) would later do, for example visiting Harvard in 1867 to give the Lowell Lectures—which D'Arcy (junior) would also give, in 1936, 69 years later.
At the age of 11, D'Arcy went to the school where his father had previously taught. He did well in academic studies, but also organized a natural history ("Eureka") club, where he and his friends collected all sorts of specimens. And by the end of his time at school, he published his first paper: the 11-page (with photographs) "Note on Ulendron and Halonia," describing the regular pattern of growth scars on two kinds of fossil plants.
At 18, D'Arcy started at Edinburgh University as a medical student. His grandfather—while distinguished—was not wealthy, with the result that D'Arcy had to support himself by tutoring Greek and writing articles for the Edinburgh-published Encyclopedia Britannica (the 9th edition, from 1889, contains an extensive article by D'Arcy on John Ray, a British naturalist of the 1600s). But D'Arcy's real passion at the time was the then-hot field of paleontology, and after two years he abandoned his medical studies—and left to instead study Natural Science at the place his father had been years earlier: Trinity College, Cambridge.
D'Arcy did well at Cambridge, had an interesting circle of friends (including the future co-author of Principia Mathematica, Alfred North Whitehead), and quickly became something of a fixture in the local natural history scene. This led Macmillan & Co. to commission D'Arcy (still an undergraduate) to produce his first book: a translation from German of Hermann Muller's The Fertilization of Flowers. The publisher thought that the book—which was a fairly traditional work of descriptive natural history, based in part on observing about 14,000 visits of insects to flowers—would be of popular interest, and (in one of his last published appearances) got no less than Charles Darwin to write a preface for it:

At Cambridge, D'Arcy hung out a lot at the new Museum of Zoology, and was particularly influenced by a young professor named Frank Balfour who studied comparative embryology, and for whom a new Department of Animal Morphology was being created—but who died trying to climb Mont Blanc right when D'Arcy was finishing Cambridge.
D'Arcy began to pursue all sorts of projects, giving lectures on topics such as "Aristotle on Cephalopods," and making detailed studies of "hydroid zoophyte" specimens (aquatic animals like sea anemones that look like plants) brought back from expeditions to the Arctic and Antarctic. He applied for a fellowship in Cambridge, but—like his father before him—didn't get it.
In 1884, though, the newly created and new-thinking (non-religious, co-ed, young professors, ...) University College in Dundee, Scotland, advertised for a professor of biology (yes, combining zoology and botany!). D'Arcy applied, and got the job—with the result that at age 24 he became a professor, a role in which he would remain for nearly 64 years.
D'Arcy the Professor
D'Arcy was immediately popular as a teacher, and continued to do a certain amount of rather dry academic work (in 1885 he published A Bibliography of Protozoa, Sponges, Coelenterata, and Worms, which was, as advertised, a list of about 6000 publications on those subjects between 1861 and 1883). But his real passion was the creation of his own Museum of Zoology, and the accumulation of specimens for it.
He was soon excitedly writing that "within the last week, I have had a porpoise, two mongooses, a small shark, an eel 8ft long... a young ostrich and two bagfuls of monkeys: all dead of course." His archive (among its 30,000 items) contains extensive evidence of all sorts of trading of specimens from around the world:

Credit: University of University of St Andrews Library
But in Dundee he found a particularly good local source of specimens. Dundee had long been a center of international textile trade, and had also developed a small whaling industry. And when it was discovered that by mixing jute with whale oil it could be turned into fabric, whaling in Dundee grew dramatically.
Some of the hunting they did was local. But whaling ships from Dundee went as far as Canada and Greenland (and once even to Antarctica). And befriending their captains, D'Arcy persuaded them to bring him back specimens (as skeletons, in jars, etc.) from their expeditions—with the result, for example, that his museum rapidly accumulated the best arctic collection around.
The museum always operated on a shoestring budget, and it was typical in 1886 when D'Arcy wrote that he'd personally been "working all day on a baby Ornithorhynchus" (platypus). In his early years as a professor, D'Arcy published only a few papers, mostly on very detailed matters—like the strangely shaped stomach of a type of possum, or the structure of the porpoise larynx, or the correct taxonomic placement of a duck-like dinosaur. And he always followed the prevailing Darwinian paradigm of trying to explain things either by their evolutionary connections, or by their fitness for a particular function.

D'Arcy Thompson's original zoology museum at University College, Dundee, around 1900. Credit: University of St Andrews Library
The Matter of the Alaskan Seals
In Dundee, D'Arcy joined various local clubs, like the Dundee Naturalists' Society, the Dundee Working Men's Field Club, the Homeric Club, and, later, also the Freemasons. He became quite active in university and community affairs, notably campaigning for a medical school (and giving all sorts of statistical evidence for its utility), as well as for education for the local poor. But mostly D'Arcy lived the life of an academic, centered around his teaching and his museum.
Still, as a responsible member of the community, he was called on in various ways, and in 1892, he joined his first government commission—formed to investigate a plague of voles in Scotland (conclusions included: "don't shoot hawks and owls that eat voles," and "it's probably not a good idea to set loose a 'virus' to infect the voles"). Then in 1896—at the age of 36—D'Arcy was tapped for a piece of international scientific diplomacy.
It all had to do with seals, and the fur trade based on them. When Russia sold Alaska to the US in 1867 it also sold the rights to the seals which bred on some of the islands in the Bering Sea. But by the 1890s Canadian ships (under British protection) were claiming the right to catch seals in the open ocean—and too many seals were being killed for the population to be maintained. In 1893 a treaty was made to clarify the situation. But in 1896 there was a need to analyze more carefully what was going on (and, yes, to claim what ended up being $10M in damages for Canadian/British sealers).
Lord Salisbury, the British Prime Minister at the time, who happened to be an amateur botanist, knew of D'Arcy and asked him to travel to the Bering Sea to investigate. D'Arcy had by that point traveled a bit around Europe, but this was a complex trip. At first he went to Washington, DC, dropping in at the White House. Then across Canada, and then by Coast Guard ship (and dog sled) to the seals.

Credit: Wolfram photo courtesy of University of St Andrews Library
D'Arcy did well at making friends with his American counterparts (who included the president of the then-a-decade-old Stanford University), and found that at least on the American-controlled islands (the Russian-controlled ones were a different story) seals were being herded a bit like sheep in Scotland, and that though there was "abundant need for care and prudent measures of conservation," things were basically OK. In Washington, DC, D'Arcy gave a long speech, and helped broker a kind "seal peace treaty"—that the British government was pleased enough with to give D'Arcy a (medieval-inspired) "Companion of the Bath" honor.
Statesman of Science
Being a professor in Dundee wasn't a particularly high position in the pecking order of the time. And after his Bering Sea experience, D'Arcy started investigating moving up. He applied for various jobs (for example at the Natural History Museum in London), but perhaps in part because he didn't have fancier academic credentials (like a PhD)—and also had spent so much of his time organizing things rather than doing research—he never got any of them.
He was nevertheless increasingly sought after as a kind of statesman of science. And in 1898 he was appointed to the Fishery Board for Scotland (a role in which he continued for 43 years), and the next year he was the British delegate to the first International Conference on Oceanography.
D'Arcy was a serious collector of data. He maintained a team of people at the fish market, keeping track of the catches brought in from boats:

Credit: Wolfram photo courtesy of University of St Andrews Library
And then he took this data and created graphics and statistical analyses:
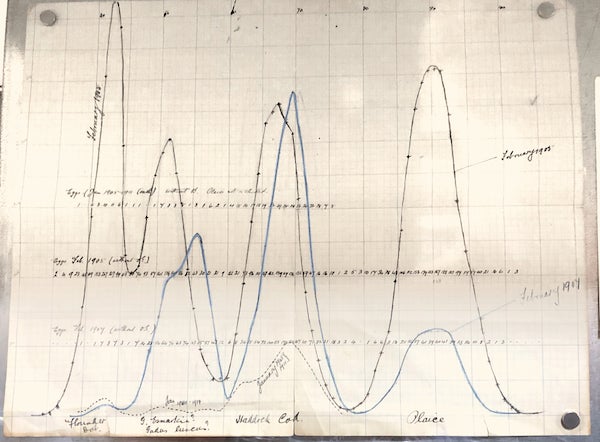
Credit: Wolfram photo courtesy of University of St Andrews Library
And over the years he became well known as a negotiator of fishing rights, both locally and internationally. He was also a collector of oceanographic data. He saw to it that there were detailed tide measurements made:
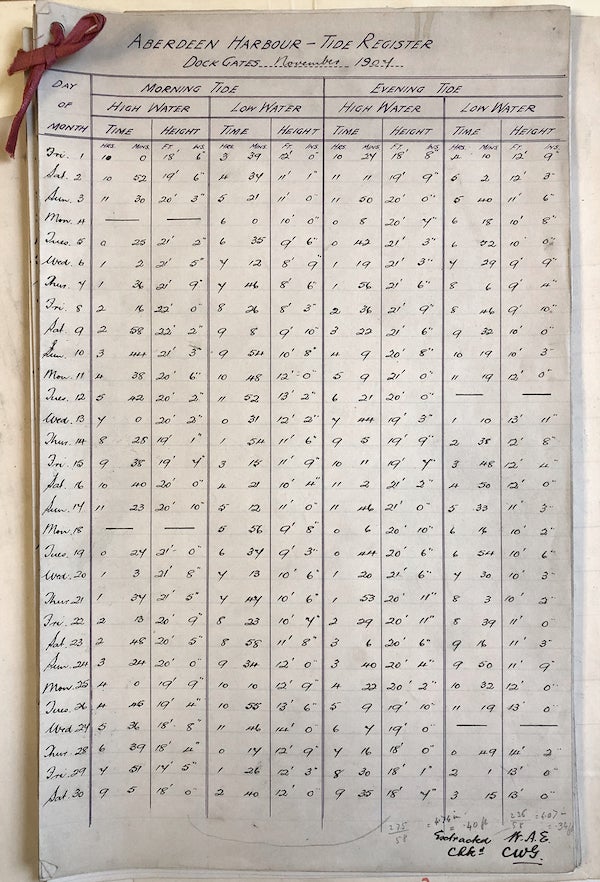
Credit: Wolfram photo courtesy of University of St Andrews Library
And had the data analyzed and decomposed into harmonic components—much as it is today:
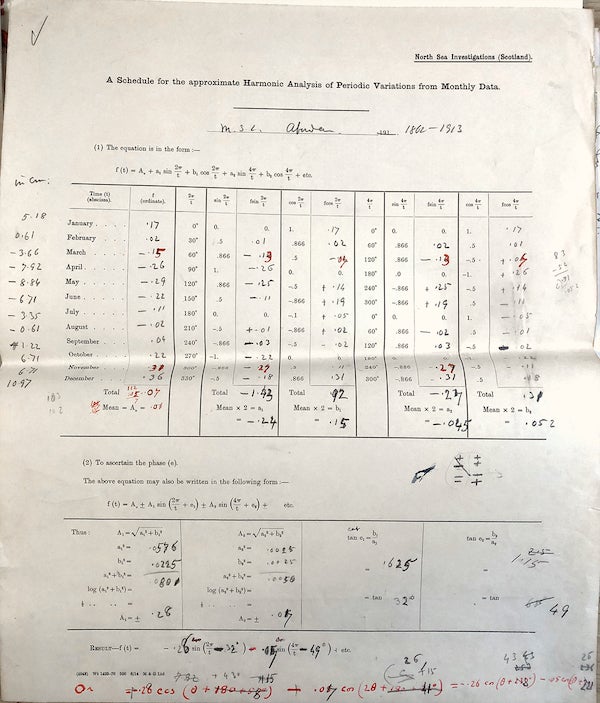
Credit: Wolfram photo courtesy of University of St Andrews Library
The Scottish government even provided for him a research ship (a steam trawler named the SS Goldseeker) in which he and his students would go around the Scottish coast, measuring ocean properties and collecting specimens.
D'Arcy the Classical Scholar
D'Arcy always had many interests. First and foremost was natural history. But after that came classics. And indeed, back in his undergraduate days, D'Arcy had already started working with his classicist father on translating Aristotle's works on natural history into English.
One of the complexities of that task, however, was to know what species Aristotle meant by words he used in Greek. And this led D'Arcy into what became a lifelong project—the first output of which was his 1894 book Glossary of Greek Birds:

It's an interesting exercise—trying to fit together clues to deduce just what modern bird some passage in classical Greek literature was talking about. Often D'Arcy succeeds. Sometimes by using natural history; sometimes by thinking about mythology or about configurations of things like constellations named for birds. But sometimes D'Arcy just has to describe something as "a remarkable bird, of three varieties, of which one croaks like a frog, one bleats like a goat, and the third barks like a dog"—and he doesn't know the modern equivalent.
Over the years, D'Arcy continued his efforts to translate Aristotle, and finally in 1910 (8 years after his father's death) he was able to publish what remains to this day the standard translation of Aristotle's main work on zoology, his History of Animals.
This project established D'Arcy as a classical scholar—and in 1912 he even got an honorary PhD (D.Litt.) at Cambridge on the basis of it. He also began a long association with what's known as Liddell & Scott, the still-standard dictionary of ancient Greek. (Liddell had been notable for being the father of Alice, of Wonderland fame.)
But D'Arcy's interests in Greek science extended beyond natural history, and into astronomy and mathematics. D'Arcy explored such things as ancient methods for computing square roots—and also studied Greek geometry.
So in 1889, when D'Arcy was investigating Foraminifera (protozoa that live in sediment or in the ocean and often form spiral shells) he was able to bring his knowledge of Greek mathematics to bear, declaring that "I have taken to Mathematics... and discovered some unsuspected wonders in regard to the Spirals of the Foraminifera!"
Towards Something Bigger
When he was 41, in 1901, D'Arcy married his stepmother's niece, the then 29-year-old Ada Maureen Drury (yes, small world that it is, she was named after "Byron's" Ada, because an ancestor had reputedly been a romantic interest of Byron's). They bought a small house somewhat outside of town—and between 1902 and 1910 they had three children, all daughters.
By 1910, D'Arcy was 50 years old, and an elder statesman of science. He kept himself busy teaching, managing his museum, doing administrative and government work, and giving public lectures. A typical lecture—given at Oxford in 1913—was entitled "On Aristotle as a Biologist." It was charming, eloquent, ponderous and Victorian:

In many ways, D'Arcy was first and foremost a collector. He collected natural history specimens. He collected Greek words. He collected academic references—and antiquarian books. And he collected facts and statements—many of which he typed onto index cards, now to be found in his archive:

Credit: Wolfram photo courtesy of University of St Andrews Library
Still, in his role as elder statesman, D'Arcy was called upon to make broad pronouncements. And in many ways the great achievement of the later part of his life was to connect the disparate things he collected and identify common themes that could connect them.
In 1908 he had published (in Nature) a two-page paper entitled "On the Shapes of Eggs and the Causes Which Determine Them." In a sense the paper was about the physics of egg formation. And what was significant was that instead of accounting for different egg shapes in terms of their evolutionary fitness, it talked about the physical mechanisms that could produce them.
Three years later D'Arcy gave a speech entitled "Magnalia Naturae: or the Greater Problems of Biology" in which he took this much further, and started discussing "the possibility of... supporting the observed facts of organic form on mathematical principles [so as to make] morphology... a true natural science... justified by its relation to mathematics."

Credit: Public Domain
In 1910, Cambridge University Press had asked D'Arcy if he'd like to write a book about whales. He said that instead perhaps he should write a "little book" about "The Forms of Organisms" or "Growth and Form"—and he began the process of assembling what would become On Growth and Form. The book had elements that drew on D'Arcy's whole range of interests. His archives contain some of what went into the assembly of the book, like the original drawings of fish-shape transformations (D'Arcy wasn't a great sketch artist):
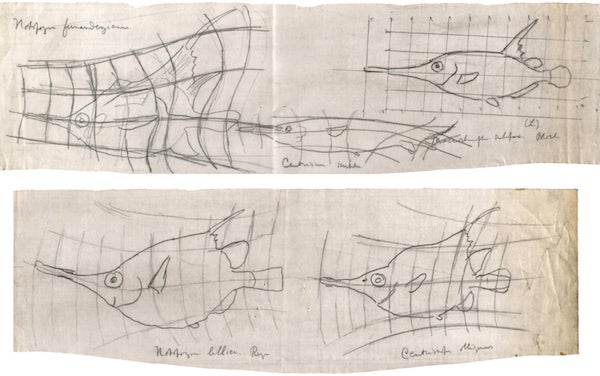
Credit: University of St Andrews Library
There were also other, more impressionistic images—like the one illustrating transformations between zebra-related animals (quagga, etc.) or one showing tortoise (?) shell structure:
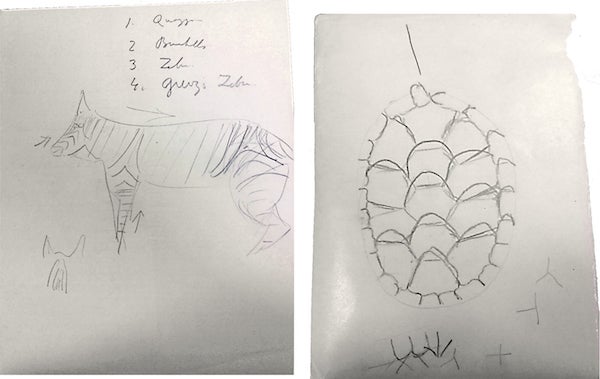
Credit: Wolfram photo courtesy of University of St Andrews Library
D'Arcy didn't contact his publisher again for several years, but in 1915—In the middle of World War I—he wrote them again, saying that he had finally finished the book "on a larger scale," and soon signed a publishing contract (that's shockingly similar to the way modern ones look):

Credit: Wolfram photo courtesy of University of St Andrews Library
It took a couple more years, between D'Arcy's last-minute changes, and paper shortages associated with the war—but finally in 1917 the book (which had by then swelled to 800 pages) was published.
The Book
On Growth and Form opens with a classic D'Arcy "Prefatory Note": "This book of mine has little need of preface, for indeed it is 'all preface' from beginning to end." He goes on to apologize for his lack of mathematical skill—and then launches, beginning with a discussion of the relation of the philosophies of Kant and Aristotle on the nature of science.

The reviews were positive, and surprisingly sensible, with the Times Literary Supplement for example writing:

Credit: The TLS Historical Archive
darcy_12.png HERE]
Further into Mathematics
D'Arcy was 57 years old by the time On Growth and Form was published—and he could have used it as a closing act in his career. But instead it seemed to make him more energetic—and seemed to encourage him to take mathematical methods as a kind of personal theme.
In his study of the shapes of biological cells, D'Arcy had gotten very interested in polyhedra and packings, and particularly in Archimedean solids (such as the tetrakaidecahedron). His archives contain all sorts of investigations of possible packings and their properties, together with actual cardboard polyhedra, still ready to assemble:

Credit: Wolfram photo courtesy of University of St Andrews Library
D'Arcy extended his interest in number theory, collecting properties of numbers a little like he'd collected so many other things:

Credit: Wolfram photo courtesy of University of St Andrews Library
He dipped into chemistry, thinking about it in terms of graphs, like those derived from polyhedra:

Credit: Wolfram photo courtesy of University of St Andrews Library
And even when he worked on history, D'Arcy used mathematical thinking, here studying the distribution of when famous people lived, in connection with writing about the Golden Ages:
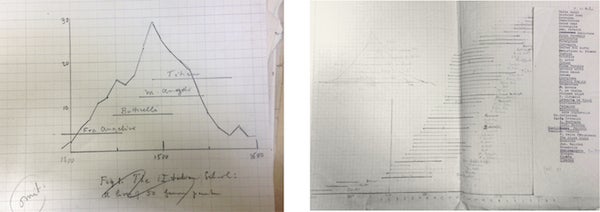
Credit: Wolfram photo courtesy of University of St Andrews Library
As an administrator, he brought in math as well, here analyzing what in today's world would be called a grading curve—and comparing exam results between different years:
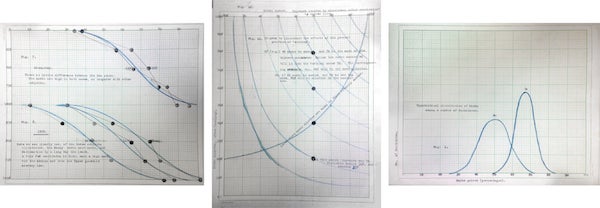
Credit: Wolfram photo courtesy of University of St Andrews Library
He worked extensively on tides and tide computations. He collected data from harbors. And came up with theories about the various components of tides, some of which turned out to be correct:
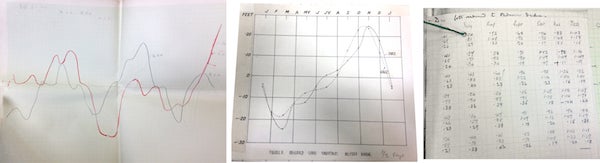
Credit: Wolfram photo courtesy of University of St Andrews Library
The mathematics he used was always a bit circumscribed—and for example he never learned calculus, even to the point of apparently getting confused about growth rates versus finite differences in plots in On Growth and Form. (There seems to be just a single sheet of calculus-like work by him in his archives, and it's simply an exercise copied without solution from the famous Whittaker & Watson textbook.)
But what about systems based on pure computational rules—of the kind that, for example, I have spent so much time studying? Well, in the archive there are things like this—perhaps a version of a space-filling curve:
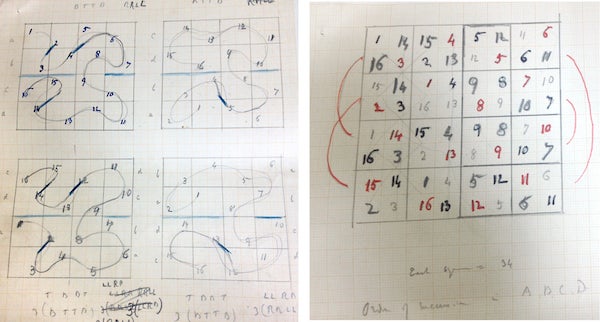
Credit: Wolfram photo courtesy of University of St Andrews Library
And back from 1897 there's a curious cardboard object that D'Arcy described as a "reasoning machine":

Credit: Wolfram photo courtesy of University of St Andrews Library
It's not completely clear what this was (though its wheel still turns nicely!). It seemed to involve a diagrammatic way of determining the truth value of a logical expression, perhaps following the work of Jevons from a couple of decades earlier. But so far as I can tell it was D'Arcy's sole excursion into the world of logic and rule-based processes—and he never connected anything like this to biology.
The Later D'Arcy
Before On Growth and Form, D'Arcy had published only quite sporadically. But after it, as he entered his sixties, he began to write prodigiously, publishing all over the place on a wide range of topics. He gave lectures, in person and on the radio. And he also began to receive all sorts of honors (he became Sir D'Arcy in 1937)—and was invited to events all over the world (he did a grand tour of the US in the 1930s, and was also received as a celebrity in places like the Soviet Union).
On Growth and Form was considered a commercial success. Its original print run was 500 copies (of which at least 113 are now in academic libraries around the world), and by 1923 it had sold out. The publisher (Cambridge University Press) wanted to reprint it. But D'Arcy insisted that it needed to be revised—and in the end it took until 1942 before he got the revisions done. The second edition added 300 pages to the book—Including photographs of splashes (obtained directly from Harold Edgerton at MIT), analysis of teeth, and patterns on animal coats. But the main elements of the book remained exactly the same.
D'Arcy had published a second edition of his Glossary of Greek Birds in 1936 (more birds, more interpretations), and in 1947, based on notes he started collecting in 1879, he released a kind of sequel: his Glossary of Greek Fishes. (Oxford University Press, in the flap copy for the book, says charmingly that "... it is highly improbable that there is any other scholar who has studied Greek fishes over so long a period as Sir D'Arcy Thompson...")
Even into his eighties, D'Arcy continued to travel all over the place—with his archives containing some typical travel documents of the time:

Credit: Wolfram photo courtesy of University of St Andrews Library
His travel was interrupted by World War II (which is perhaps why the second edition of On Growth and Form finally got finished in 1942). But in 1947, with the war over, at the age of 87, D'Arcy went to India for several months, notably lecturing on the skeletal structure of birds while holding a somewhat impatient live hen in a box. But in India D'Arcy's health began to fail, and after returning to Scotland, he died in June 1948—to the last corresponding about specimens for his museum.
Aftermath
D'Arcy's wife (who seemed in frail health through much of her 47-year marriage to D'Arcy) lived on for only 7 months after his death. None of D'Arcy's daughters ever married. His oldest daughter Ruth became a music teacher and administrator at a girl's boarding school, and in 1958 (when she was 56) published a biography of D'Arcy:

Credit: Wolfram photo courtesy of University of St Andrews Library
His middle daughter Molly moved to South Africa, wrote children's and travel books, and lived to the age of 101, dying in 2010—while his youngest daughter Barbara wrote a book on healing and herbalism and died in a freak river accident in 1990.
On Growth and Form was D'Arcy's most notable output, and it has been reprinted many times over the course of a hundred years. The museum D'Arcy created in Dundee was largely dismantled in the 1950s, but has now been to some extent reconstituted, complete with some of the very specimens D'Arcy collected, with labels duly signed "DWT" (yup, that's me next to the same orangutan as in the old picture of the museum):

Stephen Wolfram poses with an orangutan skeleton at the D’Arcy Thompson Zoology Museum in Dundee, Scotland. Credit: Stephen Wolfram
In 1917 D'Arcy moved from Dundee to the nearby but more distinguished and ancient university in St Andrews, where he took over another museum. It too fell upon hard times, but still exists in a reduced form.

Credit: Stephen Wolfram
And now some of the D'Arcy's specimens are being 3D-scanned (yes, that's the same crocodile):
.jpg?w=600)
Credit: Stephen Wolfram
And on a main street in St. Andrews there's still a plaque where D'Arcy lived:

Credit: Stephen Wolfram
What Was D'Arcy Like?

A portrait of D'Arcy Thompson that hangs outside the Bell-Pettigrew Museum at St Andrews University in Scotland. Credit: Wolfram photo courtesy of University of St Andrews Library
D'Arcy had an imposing physical presence. He stood 6'3" and had a large head, on which he often wore a black fedora. He had piercing blue eyes, and in his youth, he had red hair—which he grew into a large beard when he was a young professor. He often wore a long coat, which could sometimes seem moth eaten. Later in his life, he would sometimes walk around town with a parrot on his shoulder.
He was renowned as an engaging speaker and lecturer—known both for his colorful and eloquent content (he could regale the audience with the tale of a walrus he had known, or equally well discuss Aristotle's year by the seaside), and for the various physical (and biological) demonstrations he would use. Many stories are told of his eccentricities, especially by his former students. It is said, for example, that he once came to give a lecture to his students which began with him pulling a dead frog out of one pocket of his coat—and then a live one out of the other pocket. Despite having spent most of his life in Scotland, he didn't have a Scottish accent.
He was charming and jolly, and even in his eighties he was given to dancing when he could. He was tactful and diplomatic, if not particularly good at sensing other people's opinions. He presented himself with a certain modesty (for example always expressing his weakness in mathematics), and—perhaps to his detriment—did little to advocate for himself.
He led a fairly simple life, centered around his work and family. He worked hard, typically until midnight each day. He always liked to learn. He enjoyed children and the young, and would happily play with them. When he walked around town, he was universally recognized (the shoulder parrot helped!). He was happy to chat with anyone, and in later years, he carried candy in his pocket, which he gave out to children he encountered.
D'Arcy was a product of his age, but also of an unusual combination of influences. Like many of the members of his adopted family, D'Arcy aspired to be a scientist. But like his father, he aspired to be a classical scholar. He did diligent and detailed academic work for many years, in natural history, in classics, and in ancient science. But he also enjoyed presentation and lecturing. And it was in large part through his efforts to explain his academic work that he came to make the connections that would lead to On Growth and Form.
What Happened After
If you search the scientific literature today, you'll find about 4000 publications citing On Growth and Form. Their number relative to the total scientific literature has remained remarkably fairly even over the years (with a peak around the publication of the second edition in 1942, and perhaps a dip in the 1960s when genetics began to dominate biology):
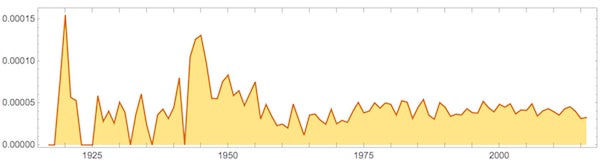
Credit: Stephen Wolfram
There's quite a diversity in the topics, as this random sample of titles indicates:

Most concern specific biological systems; some are more general. Making word clouds from titles by decade, one sees that "growth" is the dominant theme—though centered in the 1990s there are signs of the discussion that was going on about the "philosophy of evolution," and the interplay between natural selection and "developmental constraints":
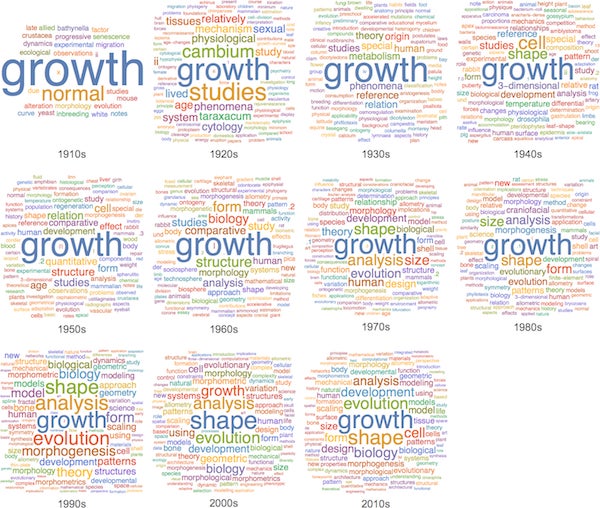
Credit: Stephen Wolfram
On Growth and Form has never really become mainstream in biology—or any other field. (It didn't help that by the 1930s, biology was firmly going off in the direction of biochemistry and later molecular biology.) So how have people found out about On Growth and Form?
Indeed, as I write this, I'm wondering: how did I myself find out about On Growth and Form? I can tell I knew about it by 1983, because I referenced it (somewhat casually) in my first long paper about cellular automata and the patterns they generate. I also know that in 1982 I bought a copy of the (heavily abridged) version of On Growth and Form that was available then. (I was thrilled in 1992 when I chanced upon a complete second edition of On Growth and Form in a used bookstore; I'd never seen the whole book before.)
But how did I first become aware of D'Arcy, and On Growth and Form? My first hypothesis today was that it was in 1977, from the historical notes of Benoit Mandelbrot's Fractals book (yes, D'Arcy had actually used the term "self-similar," though only in connection with spirals). Then I thought perhaps it might have been around 1980, from the references to Alan Turing's 1952 paper on the chemical basis of morphogenesis. I wondered if perhaps it was from hearing about catastrophe theory, and the work of René Thom, in the mid-1970s. But my best guess as of now is that it was actually around 1978, from a little book called Patterns in Nature, by a certain Peter S. Stevens, that heavily references On Growth and Form, and that I happened across in a bookstore.
I've almost never seen mentions of Patterns in Nature, but in some ways it's a simplified and modernized On Growth and Form, full of photographs comparing biological and non-biological systems, together with diagrams about how various structures can be built. But what was the path from D'Arcy to Patterns in Nature? It's a typical kind of history question that comes up.
The first thing I noticed is that Peter Stevens (born 1936) was trained as an architect, and spent most of his career around Harvard. In his book, he thanks his father, Stanley Stevens (1906-1973), who was a psychoacoustics expert, who was at Harvard from 1932 on, and who organized a "Science of Science" interdisciplinary discussion group there. But recall that D'Arcy visited Harvard to give the Lowell Lectures in 1936. So that's no doubt how Stevens, Sr. knew about him.
But in any case, from his Harvard connections came, I believe, the references to D'Arcy by evolutionary biologist Stephen J. Gould, and by John Tyler Bonner, who was the person who created the abridged version of On Growth and Form (sadly, omitting for example the chapter on phyllotaxis). I suspect D'Arcy's influence on Buckminster Fuller also came through Harvard connections. And maybe Benoit Mandelbrot heard about D'Arcy there too. (One would think that with On Growth and Form being out there as a published book, there wouldn't be need for word-of-mouth communication, but particularly outside of mainstream areas of science, word of mouth remains surprisingly important.)
But what about Turing? How did he know about D'Arcy? Well, I have at least a guess here. D'Arcy had been good friends in high school with a certain John Scott Haldane, who would go on to be a well-known physiology researcher, and who had a son named J. B. S. Haldane, who became a major figure in evolutionary biology and in the presentation of science to the public. Haldane often referenced D'Arcy, and notably introduced him to Peter Medawar (who would win a Nobel Prize for immunology), of whom D'Arcy (in 1944) would say "I do believe that more than any man you have understood what I have tried to say!"
Both Medawar and evolutionary biologist (and originator of the term "transhumanism") Julian Huxley encouraged D'Arcy to think about continuity and gradients in connection with his shape transformations (e.g. of fish). I don't know the whole story, but I suspect these two connected with C. H. Waddington, a developmental biologist (and inventor of the term "epigenetics") who interacted with Turing in Cambridge. (Small world that it is, Waddington's daughter is married to a distinguished mathematician named John Milnor, with whom I discussed D'Arcy in the early 1980s.) And when Turing came to write about morphogenesis in 1952, he referenced D'Arcy (and Waddington), then proceeded to base his theory on (morphogen) gradients.
In another direction, D'Arcy interacted with early mathematical biologists like Alfred Lotka and Vito Volterra and Nicolas Rashevsky. And though their work was heavily based on differential equations (which D'Arcy didn't really believe in), he took pains to support them when he could.
On Growth and Form also seems to have been popular in the art and architecture community, with people as diverse as the architects Mies van der Rohe, Le Corbusier, the painter Jackson Pollock and the sculptor Henry Moore also mentioning its influence.
Modern Times
So now that it's been 100 years since On Growth and Form was published, do we finally understand how biological organisms grow? Lots of work has certainly been done at the genetic and molecular scale, and great progress has been made. But when it comes to macroscopic growth, much less has been done. And a large part of the reason, I suspect, is that it's needed a new paradigm in order to make progress.
D'Arcy's work was, more than anything, concerned with analogy and (essentially Aristotelian-style) mechanism. He didn't really pursue traditional "theory" in the sense of the exact sciences. In his day, though, such theory would normally have meant writing down mathematical equations to represent growth, and then solving them to see what would happen.
And the problem is that when one looks at biological forms, they often seem far too complex to be the results of traditional mathematical equations. But starting in the 1950s a new possibility emerged: perhaps one could model biological growth as following not mathematical equations but instead rules like a program for a computer.
And when I started my systematic investigation of the computational universe of possible programs in the early 1980s, I was immediately struck by how "biological" a lot of the forms created, say, by simple cellular automata seemed:
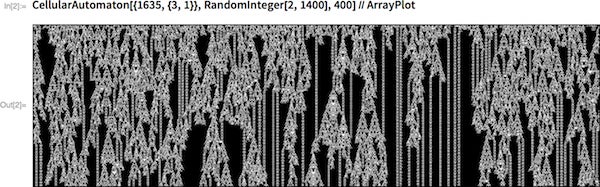
The code 1635 cellular automaton, run in Wolfram Language 11.2, generating an organic-looking pattern. Credit: Stephen Wolfram
And this is how I came to study On Growth and Form. I viewed it almost as a catalog of biological forms—that I wondered if one could explain with computational rules. I even started collecting specimens—in a very pale shadow of D'Arcy's efforts (and with no animal skeletons!):

Credit: Stephen Wolfram
Occasionally I would find one that just seemed to cry out as being from something like a program:

Stephen Wolfram's specimen of Livonia mammilla, showing a cellular-automaton-like pigmentation pattern. Credit: Stephen Wolfram
But more than that, I kept on exploring spaces of possible programs—and discovering that the range of forms they produced seem to align remarkably well with the actual range of forms one sees across biological organisms. (I looked particularly at shell shapes and patterns, as well as other pigmentation patterns, and various forms of plants.)
And in a sense what I found strongly supports a core idea of D'Arcy's: that the forms of organisms are not so much determined by evolution, as by what it's possible for processes to produce. D'Arcy thought about physical processes and mathematical forms; 60+ years later I was in a position to explore the more general space of computational processes.
And it so happened that, like D'Arcy, I ended up presenting my main results in a (big) book, that I called A New Kind of Science. My main purpose in the book was to describe what I'd learned from exploring the computational universe. And I devoted two sections (out of 114) respectively to "Growth of Plants and Animals" and "Biological Pigmentation Patterns"—producing something that looks a bit similar to On Growth and Form:

Credit: Stephen Wolfram
So, in the end, what about the fish? Well, I think I've managed to understand something about the "morphospace" of possible mollusc shells. And I've made a start on leaves—though I'm hoping one of these years to be able to get a lot more data. I've also looked at animal skeletons a bit. But, yes, I at least still don't know about the space of possible fish spaces. Though maybe somewhere inside our image identification neural net (which saw plenty of fish in its training) it already knows. And maybe it agrees with what D'Arcy thought—a hundred years ago.
For help with facts and materials I'd like to thank Matthew Jarron, Maia Sheridan, Isabella Scott, Special Collections at the University of St Andrews Library and the On Growth and Form 100 conference in Dundee/St Andrews.