This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
The cleverest card trick I’ve ever seen was performed not by a magician, but by a math professor.
A teaching assistant (let’s call him Nick), acting as magician’s assistant, recruited five student participants. Each student picked a card from a 52-card deck and handed it back to Nick, face up but invisible to Tom, the professor. Nick laid out four of these cards in front of Tom. To our astonishment, Tom immediately identified the missing fifth card.
The professor revealed the trick at the end of class. But when I came back to my dorm, bursting with excitement, my suitemate Benjamin refused to let me explain it; he had to figure this out on his own. He wandered off to his room muttering to himself, blissfully unaware that within twenty-four hours, this puzzle would prove disastrous to his dignity.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Card tricks usually rely on deception or sleight-of-hand, but this one is all about the math. Theoretically, it’s college-level math, but it boils down to something we all learned by the age of five: counting.
Although the trick is designed to spotlight the magician, a little counting reveals that the assistant is the real star of the show. After all, Nick is not just a card butler, but a collaborator: he can choose the order of the four cards to convey a message to Tom. Not only that, he can choose which four of the five cards to show. So let’s count the possibilities: five ways to choose a secret card; then four remaining choices for the first card he reveals, three choices for the next card, and so on. That gives Nick 5 x 4 x 3 x 2 x 1 = 120 options for any five-card hand.

Credit: Jesse Dunietz
The hard work, then, is on Nick, who has to strategically pick one of these 120 options; Tom just has to interpret what he’s shown. This collaborative arrangement is a lot easier than mind-reading, but it’s still easier said than done. According to the “Bookkeeper Rule” (counting principles have great names), there are 2.6 million possible five-card hands. Somehow, Nick has to be able to glance at any one of these hands and pick four cards to send a coded message to Tom, telling him both the suit and the value of the fifth card. How can Nick make the cards talk?
The evening after I saw the trick, a classmate and I were working on our counting homework (yes, really) when Benjamin appeared in the kitchen. In his trademark animated style, he chattered about how he’d worked out that Nick could choose which cards to reveal, and even devised a system for Nick to communicate with Tom. “But I’m not quite there yet – there’s one more piece of information I can’t figure out how to encode!”
As we talked, Benjamin leaned back against the wall over a large, square trash can. Gradually, he slid lower down the wall, until his hands, folded behind his back, grasped the edges of the can.
What Benjamin had figured out was a central principle of counting, known as the Pigeonhole Principle. (Told you they have great names.) Imagine a pigeon coop with nine pigeonholes in it. If ten pigeons try to rest inside, it’s a mathematical certainty that at least one slot contains more than one pigeon.

Ten is too many pigeons—there must be two pigeons in one pigeonhole! Credit: Wikimedia (CC BY-SA 3.0)
Though seemingly obvious, the Pigeonhole Principle leads to many non-obvious conclusions. For example, we know there are four suits of cards. Inescapably, when Tom’s audience draws five cards, two must share a suit.

The Pigeonhole Principle as applied to playing card suits: suits are pigeonholes, and cards are pigeons. There are only four suits, so even if the suits of four cards are different, the fifth card must be the same suit as one of the others. Credit: Jesse Dunietz
The Pigeonhole Principle as applied to playing card suits: suits are pigeonholes, and cards are pigeons. There are only four suits, so even if the suits of four cards are different, the fifth card must be the same suit as one of the others.
This suggests an easy way for Nick to communicate the hidden card’s suit. Say the five-card hand includes the J♡ and the K♡. Nick can make the jack the hidden card, and present the king as the first of the four-card code, telling Tom that the secret card is also a heart.
There’s still a key piece missing, though. Once Nick puts out that first card, he has only three cards left. There are six ways to arrange three cards – but Tom has to decide between all thirteen cards in the suit. By the same Pigeonhole Principle, six arrangements of cards can’t uniquely encode thirteen possibilities; some arrangements must be ambiguous! How can the value be jammed into the revealed cards, too?
Benjamin had worked all this out. He even had a counting-based proof that Nick can double the information payload of his message: since there are at least two cards sharing a suit, Nick can choose which one to reveal. That gives him twice as many options, six for each possible choice of the first card.
That’s still only twelve possible messages that Nick can send. Actually, though, twelve is just right—one of the cards in Nick’s chosen suit will be face-up in front of Tom! That leaves Tom with only twelve possibilities for his guess. Nick has exactly enough information-carrying capacity.
But here, Benjamin got stuck. It’s one thing to say that it must be possible to convey the necessary information; it’s quite another to do it. Benjamin just couldn’t figure out how to convert these insights into a practical code.
To make this work, we need a circle – specifically this one:
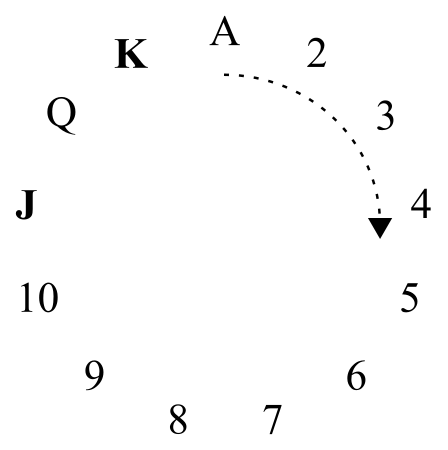
Credit: Jesse Dunietz
What’s interesting about this circle is that Nick can always make sure the hidden card is at most six steps clockwise from the first revealed card. Say the hand consisted of the five cards shown below (J♡, Q♧, 9♢, Q♤, and K♡). Nick has to choose either the jack or the king to reveal first. If he chooses the king, then the jack is eleven clockwise hops away on the circle. But if he reveals the jack, it takes only two steps to get to the king! With a strategic choice, Nick can give the magician a starting point with the true value just a few steps clockwise.
An example five-card hand. The assistant should show the first four to the magician to tell him that the last card is the K♡. Faces © Chris Aguilar, LGPL 3.0.

An example five-card hand. The assistant should show the first four to the magician to tell him that the last card is the K♡. Credit: Chris Aguilar LGPL 3.0
All that remains, then, is for Nick to tell Tom a number of hops between 1 and 6. They achieve this by agreeing in advance on an ordering of all cards in the deck. One sensible choice would be to borrow from bridge, where suits are ordered clubs, diamonds, hearts, and spades (lowest to highest), and values within a suit are ordered two through ace. In our example, the 9♢ would be “larger” than the Q♧, but smaller than the Q♤. Using this ordering, Nick and Tom establish a code that translates card sequences into numbers: small/medium/large means 1, small/large/medium means 2, etc.
What follows is complete table for translating card sequences into numbers of steps around the circle. Head over to this interactive page to try your own hand at decoding the assistant’s messages.
Card order | Meaning |
Small, medium, large | 1 |
Small, large, medium | 2 |
Medium, small, large | 3 |
Medium, large, small | 4 |
Large, small, medium | 5 |
Large, medium, small | 6 |
In our example, Nick will show the magician the first four cards shown above (J♡, Q♧, Q♤, and 9♢). The first card tells Tom that the secret suit is hearts. Because the remaining cards are ordered small/large/medium, he knows the secret value is two hops clockwise of the jack. With just these four cards, Tom can correctly guess the K♡.
Sadly for Benjamin, he never got as far as the circle trick. Hovering above the trashcan, he was suddenly struck by inspiration, and flung his arms up in the air with an “Ohhh!”
What he neglected to consider was that all his weight had been resting on those arms. Instantly, his body collapsed into the trashcan, arms and legs waggling around like an upside-down turtle. He rocked back and forth, but to no avail: he was stuck.
Naturally, my first move was to laugh hysterically and snap a photo.
Benjamin's a good sport about being stuck in the trash. He swears he wasn’t pantsless. Credit: Jesse Dunietz
I then rushed over to try to help him out, but I was wheezing so hard that all I managed to do was topple myself over, literally rolling on the floor laughing. Finally, my less-useless homework buddy stepped in. She tipped over the poor human turtle and pulled the can off Benjamin’s rear, releasing him to slink away and lick his wounds.
Counting gets you surprisingly far in math. It’s all you need to figure out whether there are two people in London with the same number of hairs on their head (there are), or the probability of a full house in poker. And at the risk of sounding like the Count, this sort of counting can be not only informative, but enjoyable (ahh-ha-ha-ha!).
Since I took that course, the instructors have apparently removed this demonstration from the lectures. No doubt they heard of the dangers their mathematical games were imposing on the rest of the university. I guess you have to be careful with counting. If you’re not careful, it can really bite you in the behind.
