This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
In the mid 1970s, Stephen Hawking made a string of unnerving discoveries about black holes—that they could evaporate, even explode, and destroy all information about what had fallen in. Physicists spent the next 40 years sorting through the wreckage. Then last year, at a conference in Stockholm, Hawking said that he and some collaborators were close to a solution to the so-called black-hole information paradox. Details, however, would have to wait.
Now the details are here—at least some of them. This week Hawking, the University of Cambridge physicist Malcolm J. Perry, and the Harvard University physicist Andrew Strominger posted a paper online in which the authors claim to make real progress toward solving the black-hole information paradox. Despite the inviting title—“Soft Hair on Black Holes”—the paper is mercilessly technical, so I asked Strominger to walk me through it. An edited transcript of our conversation follows.
Seth Fletcher: Physicists are comfortable with all sorts of insane-sounding ideas, but the idea that black holes destroy information is not one of them. Why is this something that they cannot abide?
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Andrew Strominger: Black holes destroying information means that the world is not deterministic. That is, the present doesn't predict the future perfectly, and it also can't be used to reconstruct the past. That's sort of the essence of what a physical law is. Going way back to Galileo or earlier, the idea of a physical law is that you start out with bodies in some state of motion and interacting, and you use the physical laws to determine either where they will be in the future or where they must have come from. So it's a very big thing if black holes destroy information. It's a very big thing to say that we cannot use physical laws in the way that we've been accustomed to for thousands of years to describe the world around us.
Now just because it's a very big thing doesn't mean that it's impossible. In a way, the history of physics is the history of learning that things that we thought had to be true weren’t true. We used to think that space and time were absolute. We used to think the Earth is the center of the universe. All of these things seemed completely obvious and well defined. And one by one they went by the wayside. That could happen to determinism, too. The very fact that the universe has a beginning seems to be in contradiction with determinism, because if you have nothing and then there’s something, that’s not deterministic. So determinism should be on the table. And indeed when Hawking first came out with his argument [that black holes destroyed information], it seemed like such a good argument that many or even most of the people who listened to it believed that determinism was over.
But three things happened that have changed that. The first is that you can’t just throw up your hands and say we can’t describe the universe. You need some kind of alternative—some sort of probabilistic laws or something. And Hawking and other people put out some formalism that enables you to have probabilistic laws, and so on, but it was rather quickly shown to be internally self-inconsistent.
The second thing was that experimentally it’s not plausible to say that determinism breaks down only when you make a big black hole and let it collapse because according to quantum mechanics and the uncertainty principle, you would have little black holes popping in and out of the vacuum. And so you would have to violate determinism everywhere. And the experimental bounds on that are truly extraordinary. So experimentally there are very serious consequences if there are even teeny, tiny violations of determinism.
SF: What are some of those consequences?
AS: In order to say that a symmetry implies a conservation law, you need determinism. Otherwise [symmetries] only imply conservation laws on the average. So electric charge would only have to be conserved on the average. Or energy would only have to be conserved on the average. And the experimental bounds on energy conservation are extraordinary. If you added terms to the laws of physics that violated determinism in some form, they would have to have fantastically small coefficients, one part in many trillions.
So [the black-hole information paradox] is experimentally a problem and it's theoretically a problem. Those are the first two things. The third thing was string theory. I would say up until the 1990s, the community was kind of split 50-50. But then Cumrun Vafa and I showed that certain string-theoretic black holes were capable of storing the requisite information, and they apparently also have some method of letting the information go in and out. And the fact that that worked—I mean, people had been trying for 25 years to reproduce this Bekenstein-Hawking area entropy law, or in other words, to derive the information content of a black hole from first principles. And nobody had been able to do it. And then we did it with complete accuracy. All the numbers, everything worked perfectly. And it had to be some kind of clue to something. It couldn’t just be an accident.
Now, we don’t know whether or not string theory describes the world, and we won’t know anytime soon. But this, I think, gave a lot of people, including Hawking, hope that in the real world there would be some mechanism that resembled what happens in string theory and enables information to come out of a black hole.
SF: And in a new paper that you, Stephen Hawking, and Malcolm Perry posted online this week, you argue that you’ve taken some concrete steps toward explaining how information can get in and out of a black hole. The first step in your argument is to undercut some of the assumptions underlying Hawking’s original argument using “new discoveries about the infrared structure of quantum gravity.” Can you tell us about these discoveries?

Photo by Anna N. Zytkow
AS: Infrared structure means the behavior of things that vary at the longest wavelengths. I discovered in the last two years what I think are some hugely surprising facts about the long wavelength structure not just of quantum gravity but also of quantum electrodynamics. It was clear that [these facts] had profound implications for the black hole information puzzle. They implied that some of the things that had been assumed in the argument that black holes destroy information were demonstrably wrong. And that’s how this all got started.
SF: Let’s walk through those two assumptions. One involves the final evaporation state of a black hole, and the other is the no-hair theorem.
AS: The first one has to do with the vacuum. The lowest energy thing is the vacuum. And it’s always been assumed that the vacuum in quantum gravity or in quantum electrodynamics is unique—that there’s only one zero-energy state. And what I’ve shown in the last couple of years is that that assumption is wrong. There are in fact infinitely many different vacuum states. In a way, what I showed was implicit in things that other people had said. It all started out by showing this equivalence of two different bodies of work that were done in the 1960s by Steve Weinberg and by Bondi, van der Burg, Metzner and Sachs.
In my earlier papers, I understood that this negated Stephen’s [original black-hole information-loss] argument—that it showed that one of the assumptions was wrong. But I hadn’t started the exploration of them in any detail because I had to fill out that story better. What’s happening now is that we’re starting to look in detail at exactly how this story is implemented when there’s a black hole around.
SF: Stephen Hawking is an author on this paper, so I take it he agrees that his original argument was flawed in this way.
AS: Right. I think that’s why he got excited. People have made all kinds of crazy criticisms of his argument, and to the best of my impressions, he’s correctly objected to all of them. But this one, he heard it and he seemed to immediately agree that this was the key. In fact, as you’ve learned from what happened at Stockholm, he’s more certain than I am that this is the missing link in understanding black hole information. I’ve been surprised so many times in my career about how things turn out that I'm not making any predictions. But there is a logical stream that we are following through now, and we’re going to see what its implications are. I’m sure there are going to be more surprises. But this is a first step in working out those implications.
SF: The next step in the paper seems crucial: you say that the no-hair theorem is unfounded, and that, in fact, black holes have “soft hair.”
AS: Right. In my earlier work I said that just by these conservation laws that I discovered, black holes must have some kind of hair. But I didn’t really know how it could be described in equations. And that’s what we understood here: how to describe it and how to do calculations.
SF: In the new paper, “soft hair” refers to “soft” photons and gravitons. What does “soft” mean in this context?
AS: Soft means not very much energy, or zero energy. That usage has been around since maybe the 1960s. The crucial subtlety is if you take the vacuum and you add to it a photon with some energy E you get a new state. It’s a different quantum state with energy E, and it has a different angular momentum because the photon has a spin. But now suppose you consider a limit where that energy goes to zero. Then you’re adding to the vacuum something that has no energy. So it’s still a zero energy state, but you’ve changed its angular momentum. Is that a new state, or the same state, or what? How are we supposed to think about that?
The first thing you have to do is to be very precise about what you mean about two states being different. And what I did, in a way that I think the world of theoretical physicists agrees with, is I made all of this very precise. And I showed that it is in fact a different state, and that the different states are related by symmetry. And associated with this symmetry there are conservation laws. I think there’s general acceptance that these papers are correct.
So that’s what a soft particle is. It’s a particle that has zero energy. And when the energy goes to zero, because the energy is [proportional to the] wavelength, it’s also spread over an infinitely large distance. If you like, it’s spread over the whole universe. It somehow runs off to the boundary. What we learn from that is that if you add a zero-energy particle to the vacuum, you get a new state. And so there are infinitely many vacua, which can be thought of as being different from one another by the addition of soft photons or soft gravitons.
What we showed in this present paper is that this is also true for black holes. And that’s the sense in which black holes have hair: they can have different numbers of soft photons or soft gravitons on them.
SF: In the paper, you argue that these particles, which together form the soft hair, are deposited on the black hole by something called “supertranslation.” Can you explain that process?
AS: The horizon of a black hole has the weird feature that it’s a sphere and it’s expanding outward at the speed of light. For every point on the sphere, there’s a light ray. So it’s composed of light rays. But it doesn’t get any bigger and that’s because of the force of gravity and the curvature of space. And, by the way, that’s why nothing that is inside a black hole can get out—because the boundary of the black hole itself is already moving at the speed of light.
There’s this symmetry of a black hole that we all knew about in which you move uniformly forward and backward in time along all of the light rays. But there’s another symmetry, which is the new thing in this paper (though various forms of it have been discussed elsewhere). It’s a symmetry in which the individual light rays are moved up and down. See, individual light rays can’t talk to each other—if you’re riding on a light ray, causality prevents you from talking to somebody riding on an adjacent light ray. So these light rays are not tethered together. You can slide them up and down relative to one another. That sliding is called a super-translation.
And in a way, it looks like you're not doing anything. Think of a bundle of infinitely long straws and you move one up and down relative to the other. Are you doing anything, or not? What we showed is that you are doing something. It turns out that adding a soft graviton has an alternate description as a super-translation in which you move some of these light rays back and forth relative to one another.
That’s super-translations on black holes. Super-translations were introduced in the 1960s, and they were talking not about the light rays that comprise the boundary of spacetime at the horizon of a black hole but the light rays that comprise the boundary of spacetime out at infinity. The story started by analyzing those supertranslations.
SF: So the soft photons and gravitons implanted by supertranslations store information in that they are “quantum pixels” on an information-storing “holographic plate.” [Editor’s note: For a quick primer on the holographic principle, watch this video.] In what way do they store information? What does it mean for a zero-energy photon to be “on” the horizon and to hold information about a particle that fell in?
AS: Let me go back to the soft photons or gravitons in flat space. As the energy of a particle goes to zero, its wavelength spreads out over a larger and larger region. And when its energy is zero, there’s a sense in which you can think of it as living on the boundary of spacetime. Now the horizon of a black hole is a three-dimensional surface. There are the two angular directions around a sphere. And then there is the timelike direction, which is actually lightlike because the horizon is moving at the speed of light. And that lightlike direction has a boundary. If you go to the end of those light rays there’s a boundary. And that boundary is where the hologram lives. So the soft photons or gravitons—when you add them to the black hole—they can be thought of as living at that boundary.
We show that when a charged particle goes in, it adds a soft photon to the black hole. So it adds hair to the black hole. And more generally if any particle goes in—because all particles carry mass and are coupled to gravity—they always add a soft graviton. So there’s a kind of recording device. These soft photons and gravitons record information about what went into the black hole—infinitely more information than we previously believed is recorded by this mechanism. Now whether all information is recorded by this mechanism… I'm pretty sure the answer to that is no, but there are generalizations of this mechanism and then it’s a lot more confusing.
SF: Okay, so in-falling particles deposit soft particles, or hair, on the horizon of the black hole. What about at the first infinitely tiny fraction of a second after a black hole forms? Does it have any of these soft particles on its horizon? Are there any there from the beginning saying something about what went in to form the black hole?
AS: Let me make a statement first just about the vacuum that has an obvious extension to black holes. I can say it more clearly and with more certainty for the vacuum. If you add a soft photon to the vacuum, you get a new state that has one more soft photon than the old state. The relative number of photons by which two different vacuum states differ is a well-defined question. But the absolute number is not. I can say vacuum A has one more soft photon than vacuum B, but I can’t say which one of them has none. That’s a kind of arbitrary convention. So I haven’t really carefully addressed the question in the way you’ve posed it, but I’m guessing that there’s not going to be any meaning to the question “which is the black hole with no soft photons?” You can say some have more or some have less. You can say how many particles you would have to throw in for black hole A to have the same number of soft photons as B. But there’s no absolute notion there.
This was part of the subtlety, right? Three or four years ago, and even now, people who haven’t been following my papers might say that the vacuum with the soft photon is the same with the vacuum without a soft photon. This thing is spread out to infinity and it doesn’t mean anything. But one of the lessons we’ve learned is that the boundaries of spacetimes at infinity are very important to carefully keep track of, especially when you want to study something like black hole information.
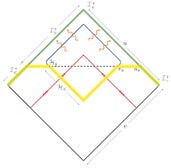
Penrose diagram of a semiclassical evaporating black hole, as presented in "Soft Hair on Black Holes." Illustration by Prahar Mitra
SF: So the information is stored on the surface. What happens when the black hole evaporates?
AS: We talk about adding soft photons to the black hole. If you compare two black holes that differ only by the addition of a soft photon that doesn’t change the energy, they’re different black holes. And then you let them evaporate. They should evaporate into something different. And indeed we give an exact formula, which is one of the main results of our paper for the difference in the quantum state resulting from a black hole with or without a soft photon.
SF: You write in the paper that there is a suggestive relationship between the minimum size of these soft hairs and the Planck length and the Hawking-Bekenstein formula, which relates the entropy of a black hole to the area of its event horizon.
AS: The area-entropy law that [Jacob] Bekenstein and Hawking derived 40 years ago makes a prediction. If we have all the ingredients for understanding quantum black-hole dynamics, it makes a prediction for how many holographic pixels there are. That has to come out exactly right. And it won’t come out exactly right until we get all the details right.
One thing that bothered us about this right from the very beginning is: Why doesn’t this allow an infinite amount of information? We don’t want an infinite amount of information. Ultimately we’d like to somehow use this to recover the Hawking- Bekenstein area entropy law. It looked like we were getting an infinite amount of hair because you seem to be able to have these soft photons that had an angular localization that was arbitrarily small. But there’s no physical way to excite one of those. So those are not physically realizable states of the black hole.
SF: Those smaller than the Planck length?
AS: Those smaller than the Planck length. I wouldn't know how to implant such a hair.
It’s very important to note that there have been lots of proposals trying to understand black hole entropy which get the area correct—which get the proportionality to the area correct—but don't get the one-quarter [term in the equation] correct. The real acid test, which we haven't passed, is getting that one-quarter. That's what string theory was able to do, and that was what turned the tide on a lot of thinking about this problem. But we haven’t gotten the one-quarter here.
SF: Is there a clear road ahead?
AS: I’ve got a list of 35 problems on the board, each of which will take many months. It’s a very nice stage to be in if you're a theoretical physicist because there are things we don’t understand, but there are calculations that we can do that will definitely shed light on it. I alluded to this briefly, but there’s something much richer and bigger and at the same time more enigmatic than the supertranslations called the superrotations.
SF: Superrotations?
AS: They are another kind of symmetry at infinity where you don’t just shift the light rays up and down, but you move them relative to one another. You interchange them. If we can make sense of them, they’re going to be more important. But they’re a much newer thing. Supertranslations were understood in the 1960s. The superrotations are something that people just started to look at about ten years ago. But we’ve learned a lot about the superrotations in the last two years.
I also think that there is a very vital connection with studies that people have been doing of entanglement entropy. That needs to be incorporated into this general framework. So there are many very concrete things to do at this point.
