This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Mathematicians named a mathematical object after me. It’s called the Horgan surface, or, alternatively, Horgan non-surface. The term was intended as an insult, but I’m honored anyway. Here’s the backstory, which is also about upheavals in mathematics, the purest of all truth-seeking endeavors.
In 1993, when I was a full-time staff writer for Scientific American (not a humble blogger, as I am now), my boss ordered me to write an in-depth report on mathematics. I resisted the assignment. In college, I was an English major. I took a single math course, on calculus. I could handle short news stories about Fermat's last theorem, which had just been solved, or the Mandelbrot set, but a major article would be too hard. My boss insisted.
I began reading books and articles and interviewing prominent mathematicians, and eventually I realized I had a story. A big one. For millennia, proofs had served as the gold standard for mathematical truth--and knowledge in general. What could be truer than the Pythagorean theorem? But mathematics was changing in ways that undermined the status of conventional proofs.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
One problem was the growing complexity and specialization of mathematics, which made confirmation of some alleged proofs difficult. A case in point was Andrew Wiles’s proof of Fermat’s last theorem. Only a handful of experts were qualified to evaluate the dense, 200-page proof when it first appeared. (It turned out to have an error, which Wiles eventually corrected.)
At the same time, funding agencies were pressuring mathematicians to work on applications like cryptography and artificial vision. In applied mathematics the motivating question shifts from Is it true? to Does it work? Math becomes less a source of illumination and beauty, practiced for its own sake, than a tool, a means to a practical end.
Increasingly, mathematicians were relying on computers to carry out arduous calculations, simulate objects and run experiments. Some advocated acceptance of so-called probabilistic proofs, which have only a certain likelihood of being true. Others urged that proofs be written in a form that can be checked by computers rather than fallible humans.
Traditionalists deplored these trends, asserting that proofs reliant on computers were not really proofs at all. But influential figures were behind the changes. One was William Thurston, who in 1982 won a Fields Medal—the mathematical equivalent of a Nobel Prize—for delineating links between topology and geometry.
Thurston, who served as a major source for my article, advocated a more free-form, “intuitive” style of mathematical research, communication and education, with less emphasis on conventional proofs. He sought to convey mathematical concepts with computer-generated models, including a video that he called “Not Knot.”
“That mathematics reduces in principle to formal proofs is a shaky idea” peculiar to the 20thcentury, Thurston told me. Ironically, he pointed out, Bertrand Russell and Kurt Godel demonstrated early in the century that mathematics is riddled with logical contradictions. “Set theory is based on polite lies, things we agree on even though we know they're not true,” Thurston said. “In some ways, the foundation of mathematics has an air of unreality.”
“The Death of Proof,” illustrated by a still from “Not Knot,” was the cover story of the October 1993 Scientific American. The subtitle said: “Computers are transforming the way mathematicians discover, prove and communicate ideas, but it there a place for absolute certainty in this brave new world?”
My introduction stated: For millennia, mathematicians have measured progress in terms of what they could demonstrate through proofs—that is, a series of logical steps leading from a set of axioms to an irrefutable conclusion. Now the doubts riddling modern human thought have finally infected mathematics. Mathematicians may at last be forced to accept what many scientists and philosophers already have admitted: their assertions are, at best, only provisionally true, true until proved false.
The backlash—mostly in the form of letters, since blogs hadn’t been invented yet--was as intense as any in my career. Mathematicians charged me with misrepresentation and exaggeration, especially in my choice of headline and cover art. Although I had quoted critics of computer-generated evidence and other trends, many mathematicians seemed to think that I was advocating—even inventing-- these challenges to traditional proof rather than simply reporting on them.
One vehement critic was David Hoffman, who had been a source for my article. Hoffman used computer models to explore minimal surfaces, which are the smallest possible areas or volumes bounded by a given curve or membrane. My article included a photo of Hoffman and images he had generated with a computer. “We gain a tremendous amount of intuition by looking at images of these surfaces on computers,” Hoffman told me. I also quoted him insisting that proofs remained the ultimate goal of research.
In a letter to the editor Hoffman wrote: “The Death of Proof” by John Horgan defies logic and accuracy in favor of controversy and sensationalism… I am very much in favor of the use of computer graphics in mathematical research and communication, but is there one respectable mathematician willing to explain and defend the notion of video proofs as a replacement for traditional mathematical methods?
Hoffman was still irate in 1998 when he reviewed my first book, The End of Science, for Notices of the American Mathematical Society. Hoffman, not unreasonably, saw "Death of Proof" as warmup for The End of Science. As he put it, my “ten-page mathematics-as- we-knew-it-is-over article was merely a finger exercise for a full-scale requiem for science.”
Hoffman was appalled that End of Science had been getting so much attention. He accused me of “a clear antipathy toward mathematical thinking and a fundamental misunderstanding of the uses of mathematics in science.” He devoted a chunk of his seven-page review to defending string theory against my attacks. He suggested that CERN’s Large Hadron Collider might soon produce evidence for string theory--which needless to say hasn’t happened.
Hoffman compared me to the apocryphal 19th-century patent commissioner who quit his job because everything had been invented. He wrote: “People who write about, think about, and do science and mathematics at the end of the twenty-first century will not have to dredge up half-true stories of patent commissioners to point out the shortsightedness of their post-postmodern critics. They will have Horgan’s End to kick around.” I certainly hope so.
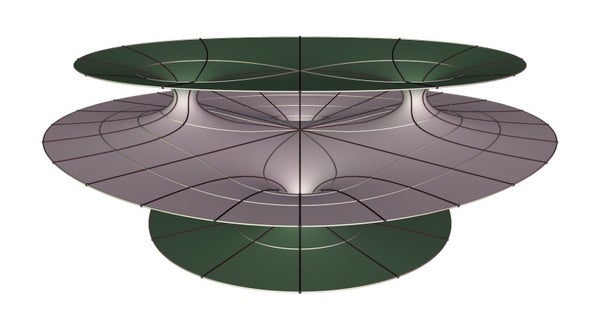
.jpg?w=712)
Credit: Matthias Weber
Meanwhile Hoffman had continued doing research on minimal surfaces. Shortly after “Death of Proof” appeared, he and Hermann Karcher explored a variant of a new kind of surface. Computer modeling suggested, at first, that the object was a genuine minimal surface, but further investigation seemed to reveal gaps (see above). Hoffman and Karcher named the object the “Horgan surface” because they saw it as a refutation of the notion that computer models can replace rigorous proofs. They discussed the Horgan surface in a paper, “Complete Embedded Minimal Surfaces of Finite Total Curvature.” A preprint appeared in 1995, and in 1997 the paper was included in volume 5 of Encyclopedia of Mathematical Sciences.
I pieced this history together from writings of mathematician Matthias Weber, which I recently discovered while self-Googling. In 1998 Weber published a paper, “On the Horgan minimal non-surface,” in Calculus of Variations and Partial Differential Equations. Hoffman and Karcher coined the phrase “Horgan surface,” Weber noted, as “a small revenge” for “Death of Proof.” Weber added that other mathematicians “were amused but asked for a nonexistence proof.”
I want to point out an irony here. Hoffman and Karcher, annoyed by my disrespect toward proof, presented no proof for their conjecture that the Horgan surface is actually a pseudo-surface! Weber supplied it. In his paper, he presented “a very simple nonexistence proof of the most symmetric Horgan surface”—or non-surface, as he preferred to call it.
Recently, Weber described the Horgan non-surface and presented images of it in two blog entries (here and here). Weber calls the non-surface “a simple, non-trivial example” of an apparent minimal surface that turns out not to be one. That “non-trivial” makes me irrationally proud.
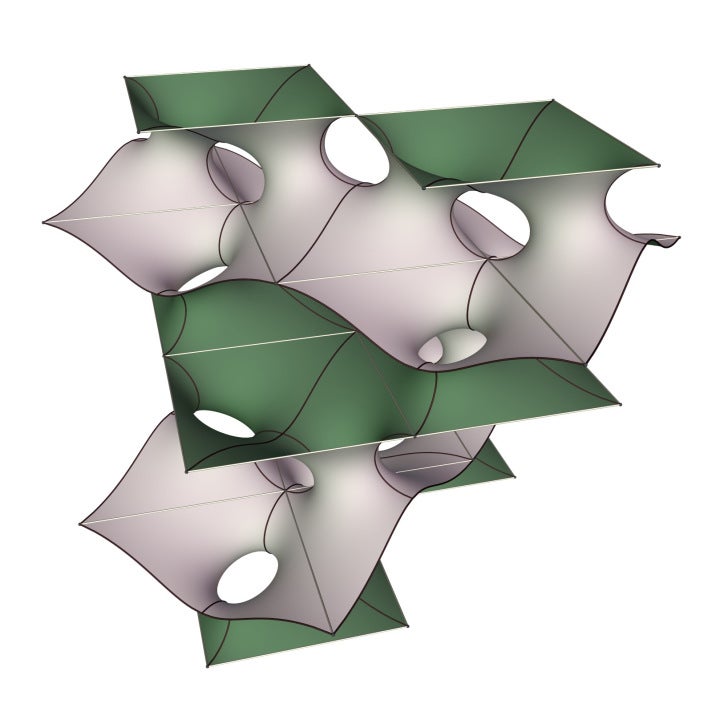
Credit: Matthias Weber
So does the fact that Weber has proved the existence of a “triply periodic Horgan surface” that is a genuine minimal surface (see above). “This is another reason why the Horgan surface is significant,” Weber told me. “The surface is on the borderline of existence (or half dead, if you want…), and slight changes to the rules can tip it one way or the other.”
Mentions of the Horgan surface can also be found in "An Embedded Minimal Surface with no Symmetries,” Journal of Differential Geometry, 2002, at the Wolfram Demonstrations Project and on my Wikipedia page. Contributors to my page, probably hostile mathematicians, have always given "Death of Proof" disproportionate attention. Someone recently added a reference to the Horgan surface, emphasizing that the coinage was “sarcastic.”
Do I regret “Death of Proof”? Hell no, no more than I regret The End of Science, which still provokes controversy. I’m thrilled that something in the realm of eternal Platonic forms has been named after me, if only sarcastically. I’m even more gratified that mathematicians continue to cite “The Death of Proof,” if only to bash it. One of my most vociferous critics, Steven Krantz, notes in his 2011 book The Proof Is in the Pudding that my article’s main claims “are well worth considering.” Thanks for the compliment, Steve.
Weber, who was a postdoc when “Death of Proof” was published, says he “would love to see” a “Death of Proof Reloaded.” He elaborates, “Ideally, you should sit together with David Hoffman, have a conversation about what happened back then and where proofs, truths, journalism, and mathematics are today, and then publish it, uncensored.” I emailed Hoffman and asked if he would do a Q&A with me, promising that I would print his answers verbatim. The co-discoverer of the Horgan surface “respectfully” declined.
Mathematics continues to be roiled by debates over alleged proofs--for example, of the Riemann Hypothesis and ABC Conjecture. And advances in computers, and especially artificial intelligence, pose an even greater challenge to traditional mathematics than they did in 1993, according to Weber. “One can easily imagine specialized software surpassing mathematicians” as constructors of proofs, he said. “When that happens, the Death of Proof you mused about will have been averted. A Pyrrhic victory, I guess.”
I recently asked Michael Harris, a mathematician-acquaintance, to give me a paragraph on how “Death of Proof” has held up. Harris replied: “It so happens I've been thinking about this question quite a lot recently. I’m not sure I could give you fewer than 1,000 words, and really anything shorter than 10,000 words would just be a string of riddles.”
He was organizing a public discussion, “Mechanization of Math,” to be held at the Helix Center in New York City in October. The announcement notes that some mathematicians have proposed “a complete rethinking of the profession, requiring future proofs to be written in computer readable code. A few mathematicians have gone so far as to predict that artificial intelligence will replace humans in mathematical research, as in so many other activities.” The announcement continues:
One’s position on the possible future mechanization of proof is a function of one’s view of mathematics itself. Is it a means to an end that can be achieved as well, or better, by a competent machine as by a human being? If so, what is that end, and why are machines seen as more reliable than humans? Or is mathematics rather an end in itself, a human practice that is pursued for its intrinsic value? If so, what could that value be, and can it ever be shared with machines?
Great questions. I’ll be there, gathering material for "Death of Proof Reloaded." I'll feel obliged to make one concession. The Horgan surfaces contradict my death-of-proof thesis, but not in the way that Hoffman and Karcher intended. Mathematics may be outrunning our cognitive capacities, and mechanization may loom, but humans are still discovering and proving the existence of new things. That makes me happy.
Further Reading:
Okay, Maybe Proofs Aren't Dying After All [follow-up post]
How William Thurston (RIP) Helped Bring About "The Death of Proof"
Who Discovered the Mandelbrot Set?
Was I Wrong about The End of Science?
Beauty Does Not Equal Truth, in Physics or Elsewhere
Bayes's Theorem: What's the Big Deal?
Mind-Body Problems (free online book)
See also my Q&As with Scott Aaronson, Stephen Wolfram, Edward Witten and Peter Woit.