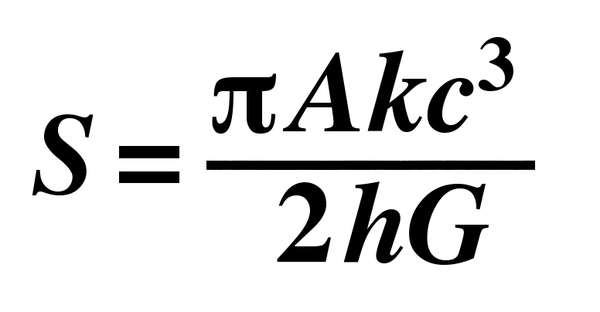This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Sad news reached Jen-Luc Piquant this morning via Jonathan Oppenheim's Twitter feed: physicist Jacob Bekenstein, a professor at the Hebrew University of Jerusalem, passed away last night. I never had the honor of meeting Dr. Bekenstein in person, but I certainly know the name. He received many well-deserved honors during his long career, most recently the 2015 Einstein Prize from the American Physical Society, awarded "For his ground-breaking work on black hole entropy, which launched the field of black hole thermodynamics and transformed the long effort to unify quantum mechanics and gravitation." According to Oppenheim, he was "a gentle soul and a brilliant physicist," adding that Bekenstein's insights into black hole entropy were "mind bogglingly remarkable."
Most people hear the term "black hole" and immediately think of Stephen Hawking, or (if they've read a lot of popular science books) Caltech physicist Kip Thorne. As well they should. But there are so many more brilliant minds grappling with the knotty implications of black hole physics, most of whom never achieve anywhere near the same level of name recognition outside the physics community. Bekenstein's was one of those minds.
Black holes are the result of a specific solution for Einstein's equations of general relativity, courtesy of Karl Schwarzschild, who began fiddling with different solutions while under heavy gunfire at the front during World War I in 1916, just after Einstein published his seminal paper – his way of taking his mind off the horrors of war. Schwarzschild was calculating the curvature of space, but hit a roadblock where the equations “blew up.” Nobody knew what that point was at the time, but today we know it as the event horizon of a black hole. John Wheeler coined the term “black hole” in 1968 to describe these objects, and we now know they are not merely hypothetical objects. They actually exist in our universe.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
If general relativity were all physicists needed to describe a black hole, there would be no problem. But they must also contend with quantum mechanics. Usually, GR applies to the physics of the very big (gravity and the curvature of spacetime), while quantum mechanics governs the realm of the very small (subatomic particles and their components). Black holes are both very massive and very dense -- infinitely dense at the singularity, where the gravity becomes so extreme that a huge mass is compressed to a teensy point. So both "rule books" can apply. And that leads to some pretty serious contradictions.
For instance, Bekenstein realized that the accepted description (at the time) of a black hole violated the second law of thermodynamics. Per Wikipedia: "If one throws a hot gas with entropy into a black hole, once it crosses the event horizon, the entropy would disappear. The random properties of the gas would no longer be seen once the black hole had absorbed the gas and settled down. One way of salvaging the second law is if black holes are in fact random objects, with an enormous entropy whose increase is greater than the entropy carried by the gas."
Calculating a black hole's entropy was an especially daunting task back in the 1970s. As I wrote earlier this year for Quanta:
Due to quirks of quantum mechanics, [black holes] radiate a small amount of heat — called “Hawking radiation” — and thus have a temperature. If black holes have temperature, they must have entropy, often described as a measure of how much disorder is present in a given system. Every physical object has entropy, and entropy must always increase, per the second law of thermodynamics. Yet the smooth, featureless picture of a black hole described by general relativity doesn’t account for its entropy, which is a key feature of its quantum mechanical description.
An object’s entropy is described by microstates: the number of ways atoms can be rearranged to achieve the same macroscale object. A scrambled egg has more entropy than an unbroken egg because the scrambled egg’s atoms can be moved around in a seemingly infinite number of ways. By contrast, the distinct yolk and white in an unbroken egg limits the possibilities for atomic-level rearrangement.
Black holes are not exempted from the laws of thermodynamics. “Entropy comes from counting the [possible] states of atoms,” explained Joseph Polchinski, a physicist at the University of California, Santa Barbara. “So black holes should have some kind of atomic structure with countable states.” The problem is that any one black hole has far more possible states than thousands of scrambled eggs.
Enter Bekenstein and his seminal 1972 paper, which demonstrated that the entropy of a black hole is exactly proportional to the size of the event horizon around it. He also proved that there is a maximum amount of information that can be stored in a finite region of space, a concept now known as the "Bekenstein bound."
So what? You may be asking. It just so happens that some of the biggest ideas in theoretical physics in the last 40 years came about because of Bekenstein's insights -- things like Hawking radiation, the black hole information paradox, the holographic principle, and the ongoing debate over the so-called black hole firewall paradox. All of which could ultimately help physicists to devise a full working theory of quantum gravity -- something that can take into account the requirements of both general relativity and quantum mechanics, which thus far just haven't played well together.
That's a pretty damned impressive impact for someone you've probably never heard of. Rest in peace, Jacob Bekenstein. You will be missed. Your ideas will live on.
References:
Almheiri, Ahmedl; Marolf, Donald; Polchinski, Joseph; and Sully, James. (2013) “Black Holes: Complementarity or Firewalls?” Journal of High Energy Physics 2.
Bekenstein, Jacob D. (April 1973) "Black holes and entropy". Physical Review D 7 (8): 2333–2346.
Bekenstein, Jacob D. (August 2003) "Information in the Holographic Universe," Scientific American, 289(2): 61.
Hawking, Stephen W. (1974) "Black hole explosions?" Nature 248 (5443): 30.
Maldacena, Juan M. (1998) “The Large N Limit of Superconformal Field Theories and Supergravity,” Adv. Theor. Math. Phys. 2: 231-252.
Strominger, A. and C. Vafa. (1996) “Microscopic origin of the Bekenstein-Hawking entropy," Phys. Lett. B 379:99-104.
Susskind, Leonard. (1995) "The World as a Hologram," Journal of Mathematical Physics 36 (11): 6377–6396.
Susskind, Leonard. The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. New York: Little Brown & Company, 2008.