This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
Monkeys! Mathematical groups! 4-dimensional geometry! Together at last!
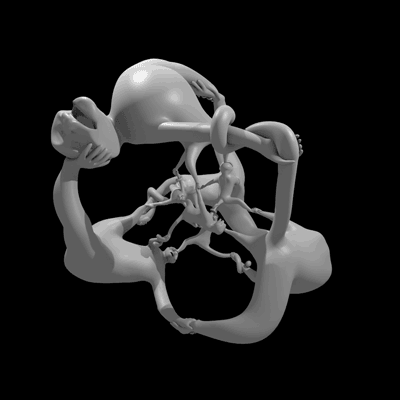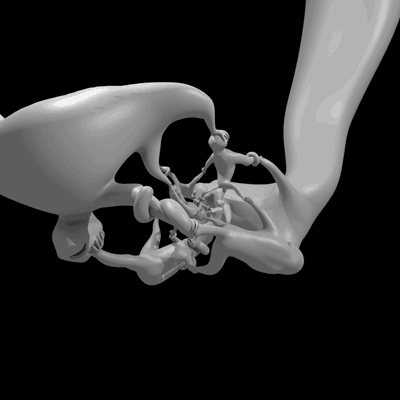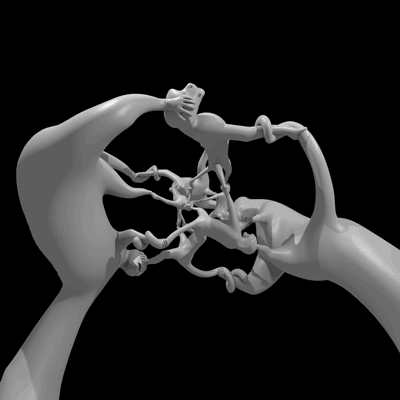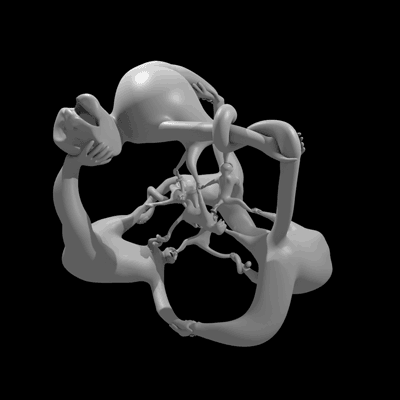
An animation of the sculpture More Fun than a Hypercube of Monkeys rotating in 4-dimensional space. (Due to the constraints of our perception, we're really viewing a projection of the 4-dimensional object.) Image: Henry Segerman and Will Segerman.
This sculpture, called More Fun than a Hypercube of Monkeys, answers an open question: has the quaternion group ever appeared as the symmetry group of an object? Thanks to mathematician Henry Segerman and mathemusician Vi Hart, the answer is now yes. Their very readable paper about the sculpture will appear in the proceedings of the 2014 Bridges math-art conference, and you can read it for free now on the preprint server arxiv.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
To understand what the monkeys mean, we need to talk about groups. The mathematical meaning of “group” is much more specific than the English meaning. At its most abstract, a group is a set of elements and an operation that eats two elements of the set and spits out a third element, with a few additional requirements. For example, when you add two integers, you get an integer. Groups also need to have an identity element, an element that leaves the other elements unchanged. For the integers, 0 plays that role. Groups need to have inverses: every element must have an inverse so that when you pair them, you get the identity. For the integers, we have opposites: +1 and -1, +2 and -2, and so on. Finally, groups need to have the associativity property: if you add three integers, say 1+2+3, it doesn’t matter whether you do 1+2 first (so you have 3+3) or 2+3 first (so you have 1+5). Either way, you end up with 6. All groups must follow that rule as well. But those are the only rules, and any set of elements with an operation that satisfies those rules is a group.
Groups do not have to be infinite like the integers. One example of a finite group is the numbers 1 and -1 with the operation of multiplication. It satisfies all the rules with just two elements. We can even think about this group visually, in terms of transformations. The element 1 leaves everything alone (it is the identity) and -1 reflects things across a line. If you have an object with bilateral symmetry, you can reflect it across the line of symmetry and the object will look the same. Hence the -1 transformation represents a symmetry of the object.

This picture of an apple is (mostly) unchanged when reflected across the blue line. Image: Evelyn Lamb, based on a photo by Rasback, via Wikimedia Commons.
If bilateral symmetry is the only symmetry a picture or object has, then the group of 1 and -1 with multiplication is called its symmetry group. But for this picture of an apple, we also have a rotational symmetry. If we rotate by 1/5 of a turn, the picture is the same. Let’s name that rotation a.

The symmetries of this apple include reflection across the blue line and the rotation labeled "a." Image: Evelyn Lamb, based on a photo by Rasback, via Wikimedia Commons.
We can perform the rotation a on the picture up to 5 times, at which point we get back to the identity. We can also combine any of those rotations with the -1 reflection. In the end, the symmetry group of this apple picture can be represented by the elements 1, -1, a, -a, a2, -a2, a3, -a3, a4, and -a4. (You can read more about why these are the only elements of this symmetry group at the Wikipedia page for dihedral groups.)
The relationship between groups and symmetry has been a useful way to study objects that have symmetries and groups themselves. In their paper, Hart and Segerman lay out a few questions about groups and symmetries:
“1. Which groups can be represented as the group of symmetries of some real-world physical object?
2. Which groups have actually been represented as the group of symmetries of some real-world physical object?
3. Are there any glaring gaps – small, beautiful groups that should have a physical representation in a symmetric object but up until now have not?”
They zero in on question #3: there is indeed a small, beautiful group, the quaternion group, that until now did not have a physical representation. It only has 8 elements: 1, -1, i, -i, j, -j, k, and -k. This is its multiplication table. (Order of multiplication matters in this group, and the left element comes before the top one. So ij=k, but ji=-k.)
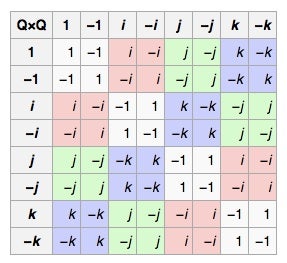
The multiplication table for the quaternion group.
The numbers 1 and -1 behave normally. The numbers i, j, and k all square to -1 (so they're kind of like imaginary numbers), and there is a cyclic relationship between i, j, and k: ij=k, jk=i, ki=j. (If you've taken physics or multivariable calculus, this may remind you of cross products.)
One reason that the quaternion group has not yet appeared as the symmetry group of a physical object or piece of art is that it is not a subgroup of the symmetry group of the plane or 3-dimensional space. In other words, there is no combination of rotations, translations, and reflections in 2 or 3 dimensions that leaves the space intact and has the structure of the quaternion group.
But because Hart and Segerman are creative, determined people, they were not dissuaded by a small detail like the constraints of 3-dimensional geometry! The quaternion group is a subgroup of the symmetry group of 4-dimensional space, so they did the logical thing and moved up a dimension. Segerman has been visualizing 4-dimensional objects using projections for a while now. (I wrote about it in 2012.) If you have a 3-dimensional object, one way you can visualize it 2-dimensionally is to aim a light source at it and look at its shadow on the wall. Segerman and his collaborators have used a similar technique, one dimension up, to make 3-d prints of projections of 4-dimensional objects. Segerman gave an hour-long talk about the technique that is available on YouTube, and he and Saul Schleimer wrote about it here (pdf).
The sculpture, which in addition to the animation above has a physical realization thanks to the magic of 3-d printing, was designed by Segerman and his brother Will. They started with the 4-dimensional analog of the cube, sometimes called a hypercube, tesseract, or 8-cell. The symmetry group of a hypercube is bigger than the quaternion group, so they had to do something to reduce the number of symmetries. That’s where the monkeys came in. In order to decrease the total number of symmetries, they put a monkey at the center of each of the 8 cubes of the hypercube.* Each monkey had two arms, two legs, a tail, and a head. This made it so there were only a few ways to twist and turn the object and still preserve the placement of simian appendages. With the correct monkey orientation, they managed to restrict the symmetries just enough to get the quaternion group. (For complete details, I urge you to read the paper.) Then, it was a matter of using Segerman's projection technique to make the monkeys a reality. Just like making shadow puppets on a wall, the projection distorts size. So the monkeys are all the same size in 4 dimensions, but their projection to 3 dimensions makes some of them look larger.
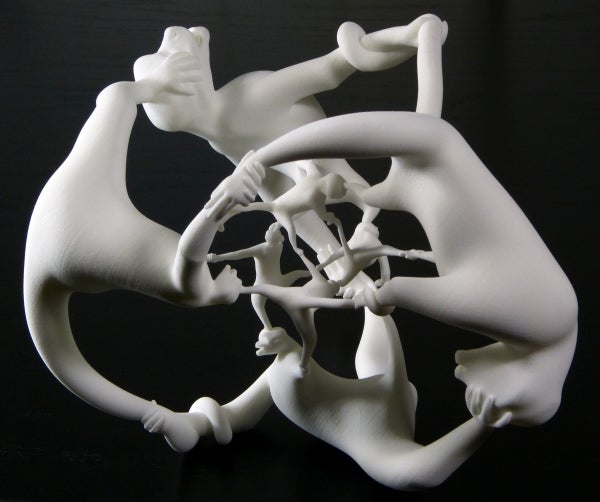
More Fun than a Hypercube of Monkeys, a sculpture with quaternion group symmetry. Image: Henry Segerman and Will Segerman.
I hope Hart, Segerman, and Segerman (and other mathematical artists) will continue to make other neglected groups into symmetry groups. I'm holding out hope for a monster group of monsters!
*Correction: This sentence originally stated that there was a monkey at every vertex of the hypercube. There is a monkey at every cube of the hypercube.