This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
A Numberphilevideo posted earlier this month claims that the sum of all the positive integers is -1/12.
I'm usually a fan of the Numberphile crew, who do a great job making mathematics exciting and accessible, but this video disappointed me. There is a meaningful way to associate the number -1/12 to the series 1+2+3+4…, but in my opinion, it is misleading to call it the sum of the series. Furthermore, the way it is presented contributes to a misconception I often come across as a math educator that mathematicians are arbitrarily changing the rules for no apparent reason, and students have no hope of knowing what is and isn't allowed in a given situation. In a post about this video, physicist Dr. Skyskull says, "a depressingly large portion of the population automatically assumes that mathematics is some nonintuitive, bizarre wizardry that only the super-intelligent can possibly fathom. Showing such a crazy result without qualification only reinforces that view, and in my opinion does a disservice to mathematics."
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Addition is a binary operation. You put in two numbers, and you get out one number. But you can extend it to more numbers. If you have, for example, three numbers you want to add together, you can add any two of them first and then add the third one to the resulting sum. We can keep doing this for any finite number of addends (and the laws of arithmetic say that we will get the same answer no matter what order we add them in), but when we try to add an infinite number of terms together, we have to make a choice about what addition means. The most common way to deal with infinite addition is by using the concept of a limit.
Roughly speaking, we say that the sum of an infinite series is a number L if, as we add more and more terms, we get closer and closer to the number L. If L is finite, we call the series convergent. One example of a convergent series is 1/2+1/4+1/8+1/16…. This series converges to the number 1. It's pretty easy to see why: after the first term, we're halfway to 1. After the second term, we're half of the remaining distance to 1, and so on.
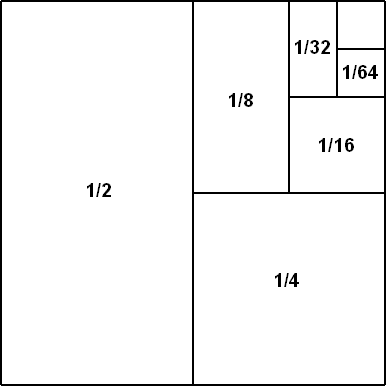
A visual "proof" that 1/2+1/4+1/8...=1. Image: Hyacinth, via Wikimedia Commons.
Zeno's paradox says that we'll never actually get to 1, but from a limit point of view, we can get as close as we want. That is the definition of "sum" that mathematicians usually mean when they talk about infinite series, and it basically agrees with our intuitive definition of the words "sum" and "equal."
But not every series is convergent in this sense (we call non-convergent series divergent). Some, like 1-1+1-1…, might bounce around between different values as we keep adding more terms, and some, like 1+2+3+4... might get arbitrarily large. It's pretty clear, then, that using the limit definition of convergence for a series, the sum 1+2+3… does not converge. If I said, "I think the limit of this series is some finite number L," I could easily figure out how many terms to add to get as far above the number L as I wanted.
There are meaningful ways to associate the number -1/12 to the series 1+2+3…, but I prefer not to call -1/12 the "sum" of the positive integers. One way to tackle the problem is with the idea of analytic continuation in complex analysis.
Let's say you have a function f(z) that is defined somewhere in the complex plane. We'll call the domain where the function is defined U. You might figure out a way to construct another function F(z) that is defined in a larger region such that f(z)=F(z) whenever z is in U. So the new function F(z) agrees with the original function f(z) everywhere f(z) is defined, and it's defined at some points outside the domain of f(z). The function F(z) is called the analytic continuation of f(z). ("The" is the appropriate article to use because the analytic continuation of a function is unique.)
Analytic continuation is useful because complex functions are often defined as infinite series involving the variable z. However, most infinite series only converge for some values of z, and it would be nice if we could get functions to be defined in more places. The analytic continuation of a function can define values for a function outside of the area where its infinite series definition converges. We can say 1+2+3...=-1/12 by retrofitting the analytic continuation of a function to its original infinite series definition, a move that should come with a Lucille Bluth-style wink.

The function in question is the Riemann zeta function, which is famous for its deep connections to questions about the distribution of prime numbers. When the real part of s is greater than 1, the Riemann zeta function ζ(s) is defined to be Σ∞n=1n-s. (We usually use the letter z for the variable in a complex function. In this case, we use s in deference to Riemann, who defined the zeta function in an 1859 paper [pdf].) This infinite series doesn't converge when s=-1, but you can see that when we put in s=-1, we get 1+2+3…. The Riemann zeta function is the analytic continuation of this function to the whole complex plane minus the point s=1. When s=-1, ζ(s)=-1/12. By sticking an equals sign between ζ(-1) and the formal infinite series that defines the function in some other parts of the complex plane, we get the statement that 1+2+3...=-1/12.

Analytic continuation is not the only way to associate the number -1/12 to the series 1+2+3.... For a very good, in-depth explanation of a way that doesn't require complex analysis—complete with homework exercises—check out Terry Tao's post on the subject.
The Numberphile video bothered me because they had the opportunity to talk about what it means to assign a value to an infinite series and explain different ways of doing this. If you already know a little bit about the subject, you can watch the video and a longer related video about the topic and catch tidbits of what's really going on. But the video's "wow" factor comes from the fact that it makes no sense for a bunch of positive numbers to sum up to a negative number if the audience assumes that "sum" means what they think it means.
.jpg?w=350)
VIa quickmeme.
If the Numberphiles were more explicit about alternate ways of associating numbers to series, they could have done more than just make people think mathematicians are always changing the rules. At the end of the video, producer Brady Haran asks physicist Tony Padilla whether, if you kept adding integers forever on your calculator and hit the "equal" button at the end, you'd get -1/12. Padilla cheekily says, "You have to go to infinity, Brady!" But the answer should have been "No!" Here, I think they missed an opportunity to clarify that they are using an alternate way of assigning a value to an infinite series that would have made the video much less misleading.
Other people have written good stuff about the math in this video. After an overly credulous Slate blog post about it, Phil Plait wrote a much more levelheaded explanation of the different ways to assign a value to a series. If you'd like to work through the details of the "proof" on your own, John Baez has you covered. Blake Stacey and Dr. Skyskull write about how substituting the number -1/12 for the sum of the positive integers can be useful in physics. Richard Elwes posts an infinite series "health and safety warning" involving my old favorite, the harmonic series. I think that the proliferation of discussion about what this infinite series means is good, even though I wish more of that discussion could have been in the video, which has more than a million views on YouTube so far!