This article was published in Scientific American’s former blog network and reflects the views of the author, not necessarily those of Scientific American
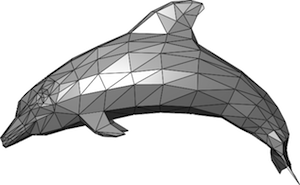
A triangulation of a dolphin. Image: Crhschn, via Wikimedia Commons.
Surfaces are complicated. Triangles are simple. That's an idea behind some methods of creating computer graphics and some advanced mathematics. If we have a surface, we can take a bunch of points on the surface and connect them into triangles to obtain an approximation of the surface. That's all well and good, but how reliable is the triangulation? How accurately does it reflect the properties of the original surface? For example, as we increase the number of triangles in the approximation of the surface, will the surface area of the triangulated surface get close to the surface area of the original surface?

Karl Hermann Amandus Schwarz, who first described the Schwarz lantern. Image: public domain, via Wikimedia Commons.
On supporting science journalism
If you're enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
In 1880, mathematician and righteous facial hair maintainer Hermann Schwarz answered this question in the negative by producing a counterexample, a surface and sequence of triangulated approximations for which the surface area of the triangulations gets arbitrarily large and hence doesn't converge to the surface area of the original surface.
Earlier this semester, I had the opportunity to go to an origami workshop put on by the local chapter of the Association for Women in Mathematics. Radhika Gupta, a graduate student here at the University of Utah, showed us how to make this counterexample, dubbed the Schwarz lantern, just by folding paper.
To make a Schwarz lantern, we start with a piece of paper.
Image: Evelyn Lamb.
We divide the length of the paper into M parts, so we get M skinny horizontal rectangles.
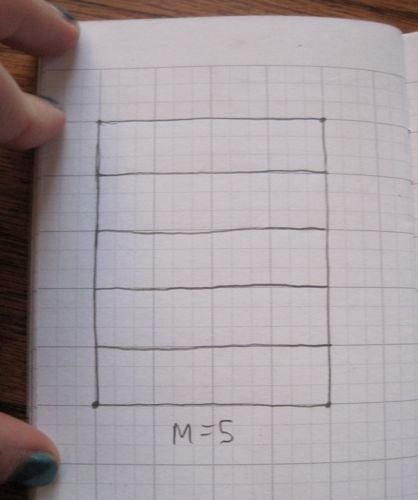
Image: Evelyn Lamb.
Then each skinny horizontal rectangle gets divided into 2N triangles by placing N points on both the top and bottom at an offset and connecting the points up into triangles. (Note that in the end, the left and right sides will be glued together, so some triangles are drawn so half is on the right side and half is on the left side before gluing.)
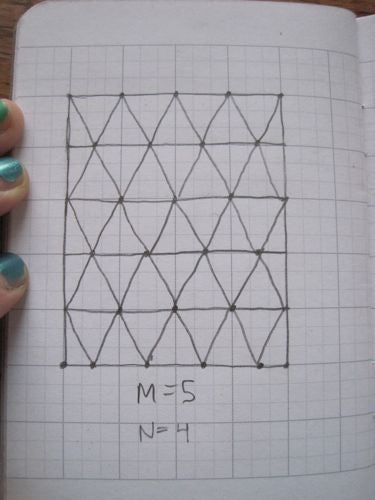
Image: Evelyn Lamb.
Now we just have to fold the horizontal lines "in" and the diagonal lines "out" and tape the right side to the left side to get a surface that is made of triangular faces but kind of looks like a cylinder. (Caution: this step is kind of hard. I had to get help from workshop leader Gupta and one of my students, who is a talented origami folder. You may also require assistance.)

A Schwarz lantern I made with a little help from my friends. The vertices (pointy bits) all lie on a cylinder. (This is not made from the piece of paper in the previous three pictures. It has many more triangles than that one did.) Image: Evelyn Lamb.
As M and N increase, the triangulation converges to the cylinder in one sense: the distance between any point on the triangulation and a point on the cylinder goes to 0 as the number of triangles increases. But depending on the ratio of N to M, the surface area of the triangulation may not converge to the surface area of the cylinder. If N is a lot larger than M (specifically, if the ratio N/M does not go to 0), the surface area of the triangulation gets arbitrarily large. Another way to think about it is that if N is very large compared to M, then as N and M increase, the cylinder you get when you fold them up gets smaller and smaller.
It's worth asking whether we should be surprised that we can create this counterexample. Should we expect triangulated approximations of our surface to have the same properties as the surface itself? When I was trying to decide whether the Schwarz lantern was mind-blowing or just interesting, I thought about what happens when we ask a similar question about curves in the plane. When we approximate a curved shape in the plane with polygons (shapes with straight sides), will the perimeter of the polygons converge to the perimeter of the curved shape? Not necessarily. Let's just think about a circle as the shape we're approximating. If we restrict our approximations to regular convex polygons (your standard issue equilateral triangles, squares, and so on) then we can approximate the circle by increasing the number of sides in the regular polygons. In that case, the perimeter of the polygons does go to the perimeter of the circle as the number of sides increases. But if we relax the rules, it's possible to draw a sequence of polygons that seem to converge to the circle but whose perimeters are stubbornly always equal to 4. For a nice explanation of that construction, see Vi Hart's video Rhapsody on the Proof of Pi=4. Although it's not a perfect analogy, I think the Schwarz lantern idea is similar to the one in that video, so in some sense its existence isn't too surprising.
For more information on the Schwarz lantern, check out Conan Wu's blog post about it or its page on Cut the Knot. Wu's post includes a printable template and instructions for making your own!

View from above a Schwarz lantern. Image: Evelyn Lamb.